Вектори і матриці
Вектори і матриці.
З впорядкованої послідовністю дійсних чисел a1, a2, .... an можна зв'язати поняття пов'язаного вектора в n-вимірному просторі і позначити як:
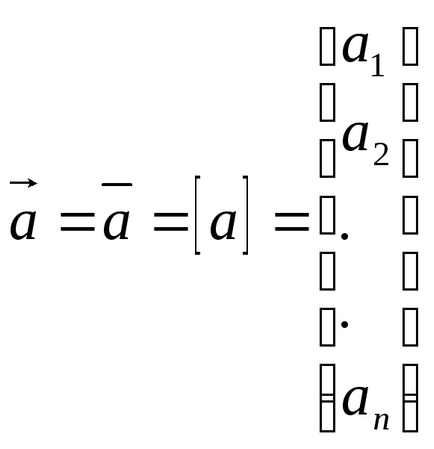
Типи і характеристики векторів.
Нульовий вектор - вектор, всі компоненти якого дорівнюють нулю.
Одиничний вектор - вектор, довжина якого дорівнює одиниці:
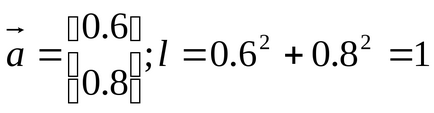
Транспонований вектор - вектор, компоненти якого розташовуються у вигляді рядка:
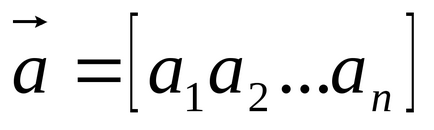
Два вектора з однаковою розмірністю рівні тоді, коли рівні їх відповідні компоненти:
Сукупність чисел розташованих в прямокутної таблиці, що складається з n рядків і m стовпців, називається матрицею і позначається як:
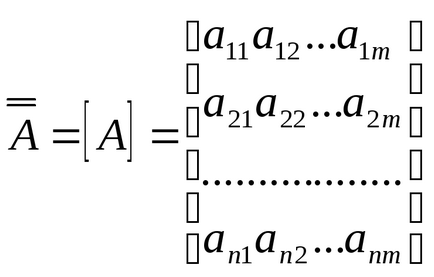
положення елемента

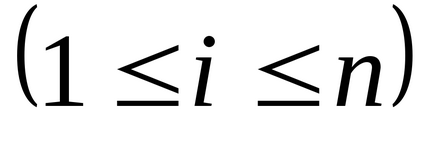
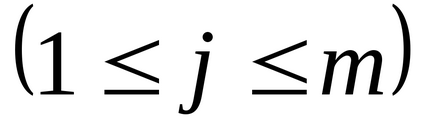
Вектор рядок - матриця, що складається з одного рядка n = 1
Вектор стовпець - матриця, що складається з одного стовпця m = 1
Квадратна матриця - матриця, у якої n = m
Верхньо трикутна - матриця, у якій
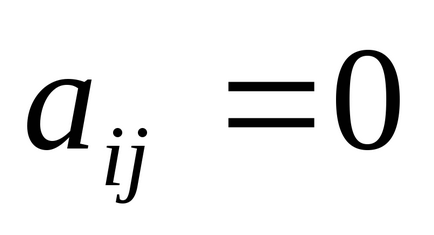
Нижньо трикутна - матриця, у якій
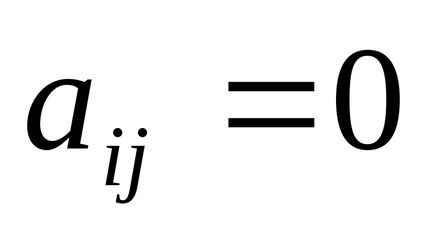
Діагональна - матриця, у якій
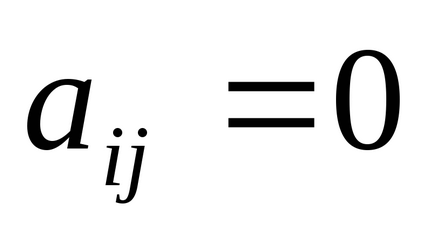
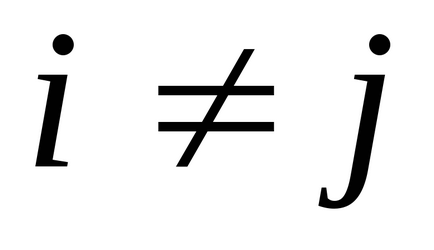
Одинична - матриця, у якій
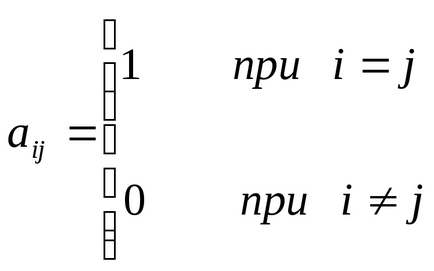
рівність матриць
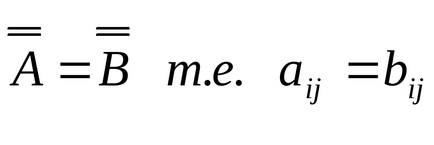
Характеристики та операції.
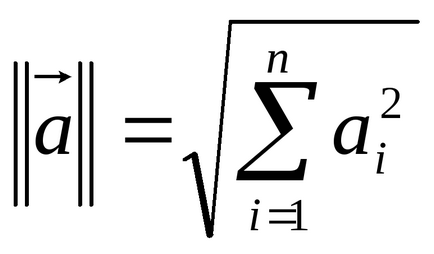
Норма матриці (евклідова).
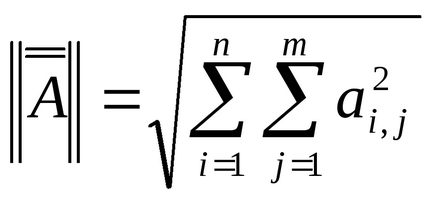
Додавання і віднімання векторів.
Додавати і віднімати можна тільки вектора з однаковою розмірністю. Результатом операції додавання (віднімання) є вектор, компоненти якого дорівнюють сумі (різниці) відповідних компонент двох інших векторів.
Додавання і віднімання матриць.
Додавати і віднімати можна тільки матриці з однаковою розмірністю. Результатом операції додавання (віднімання) є матриця, елементи якої дорівнюють сумі (різниці) відповідних елементів двох інших матриць.
Властивість операцій додавання (віднімання) матриць:
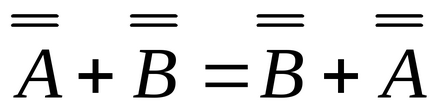
Множення вектора на константу.
Результатом множення є вектор, компоненти якого дорівнюють добутку відповідних компонент вихідного вектора на константу.
Множення матриці на константу.
Результатом множення є матриця, елементи якої дорівнюють добутку відповідних елементів вихідної матриці на константу.
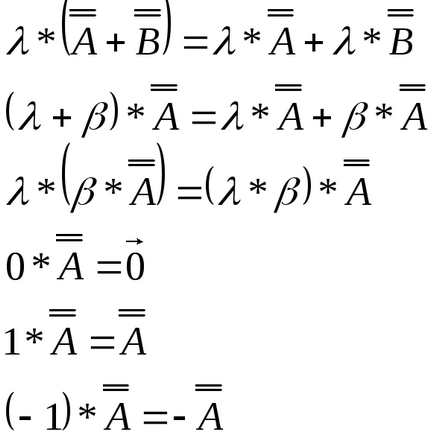
Транспонування матриці - це заміна рядків матриці відповідними стовпцями, тобто
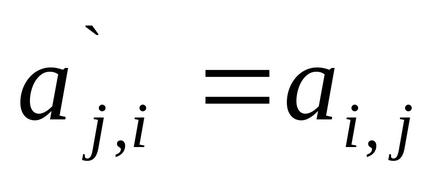
Кількість стовпців матриці A повинна дорівнювати кількості рядків матриці B.