Перетин прямої з площиною, нарисна геометрія
Завдання на перетин прямої з площиною - це одна з основних задач, з її застосуванням стикаються при розгляді перетину тел площинами і перетину поверхонь.
Знаходження точки зустрічі прямої з площиною, заданої пересічними прямими
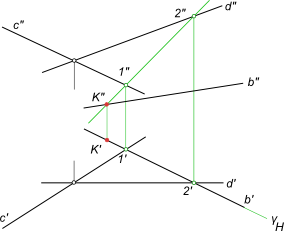
Перетин прямої з площиною
Площина і перетинає її пряма займають загальне положення.
$ K = (γ ∩ α) ∩ b $
(Γ ∩ α) = l - пряма, перетинається з прямою b.
Відділення знаходиться на перехресті прямої з площиною складаємо алгоритм знаходження їх точки зустрічі.
1) проводимо через b` горизонтальний слід γH - горизонтально-проецирующей площині γ;
2) визначаємо фронтальну проекцію лінії перетину l. допоміжної січної площини γ з даної площиною α. використовуючи для цього точки 1` і 2` (належать даній прямій), в яких горизонтальний слід γH перетинає прямі c` і d`;
3) визначаємо точку K "= l" ∩b ". Знаючи K", знаходимо K` на перетині b` з лінією проекційної зв'язку.
Знаходження точки зустрічі прямої з площиною, заданої паралельними прямими
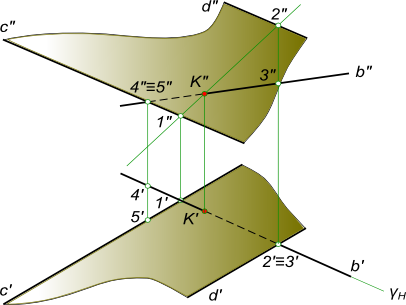
Перетин прямої з площиною
Завдання по знаходженню точки зустрічі прямої з площиною заданої слідами.
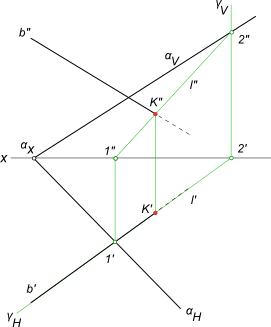
Перетин прямої з площиною
Алгоритм рішення не змінюється, якщо площину буде задана паралельними прямими або прямими, за якими вона перетинає площині проекцій (сліди площини).
При вирішенні завдань на перетин прямої з площиною в якості допоміжних площин застосовують проектують площині. Але в разі, наприклад, профільної прямої вони не приносять користі і тоді треба застосувати площину загального положення.
Знайти точку зустрічі профільної прямої AB з площиною α заданої слідами
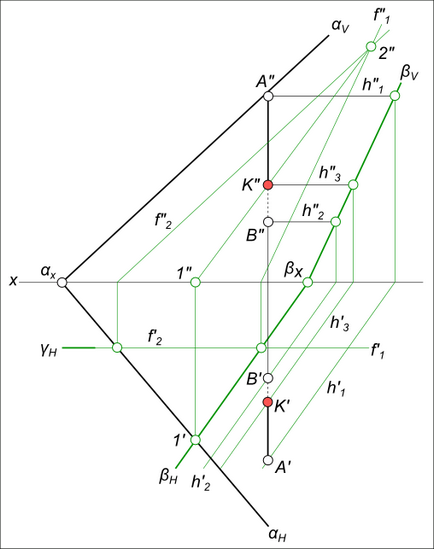
Перетин прямої з площиною
Алгоритм виконання геометричних побудов: 1) Укладаємо відрізок AB у допоміжну січну площину загального положення β; 2) Визначаємо проекції лінії перетину 1-2. допоміжної січної площини β з даної площиною α; 3) Визначаємо проекцію K "точки K на перетині 1" -2 "з прямою A" B ". Проекція K` точки K може бути знайдена: - на перетині A`B` з 1`-2`; - або як належить площинах α і β.
Знайти точку зустрічі прямої d з площиною α (b, c), визначити видимість
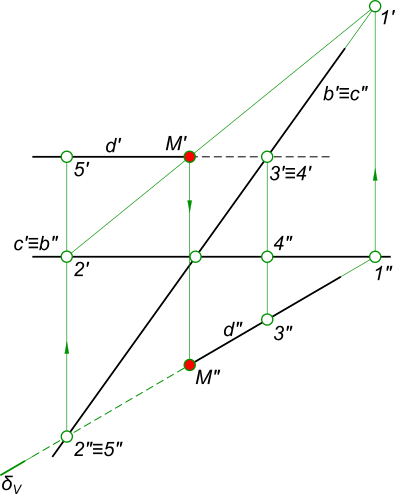
Перетин прямої з площиною
Алгоритм виконання геометричних побудов: 1) Укладаємо пряму d у допоміжну січну фронтально проецирующую площину δ; 2) Визначаємо проекції лінії перетину 1-2. допоміжної січної площини δ з даної площиною α; 3) Визначаємо проекцію K` точки K на перетині 1`-2` з прямою d`. Проекцію K "точки K знаходимо в перетині d" з лінією проекційної зв'язку.
Даний спосіб вирішення завдання - знайти точку зустрічі профільної прямої з площиною заданої слідами застосований в статті: Перетин піраміди площиною
Визначення видимості перетину прямої з площиною на площинах проекцій виконуємо, використовуючи Конкуруючі точки 2, 3 і 4, 5.