Перетин прямої з площиною і перетин двох площин
Побудова точки перетину прямої з проецирующей площиною зводиться до побудови другої проекції точки на епюрі, так як одна проекція точки завжди лежить на сліді проецирующей площині, тому що все, що знаходиться в проецирующей площині, проектується на один з слідів площини. На рис. 224, а показано побудова точки перетину прямої EF з фронтально-проектує площиною трикутника АВС (перпендикулярній площині V) На площину V трикутник АВС проектується у відрізок а'с 'прямої лінії, і точка k' буде також лежати на цій прямій і перебувати в точці перетину е'f 'з а'с'. Горизонтальну проекцію будують за допомогою лінії проекційної зв'язку. Віді-ність прямої відносно площини трикутника ABC визначають по взаємному розташуванню проекцій трикутника ABC і прямий EF на площині V. Напрямок погляду на рис. 224, а вказано стрілкою. Та ділянка прямої, фронтальна проекція якого знаходиться вище проекції трикутника, буде видимим. Лівіше точки k 'проекція прямої знаходиться над проекцією трикутника, отже, на площині H цю ділянку видимий.
На рис. 224, б пряма EF перетинає горизонтальну площину Р. Фронтальна проекція k 'точки К - точки перетину прямої EF з площиною Р - буде знаходитися в точці перетину проекції е'f' зі слідом площини Рv, так як горизонтальна площина є фронтально-проектує площиною. Горизонтальну проекцію k точки K знаходять за допомогою лінії проекційної зв'язку.
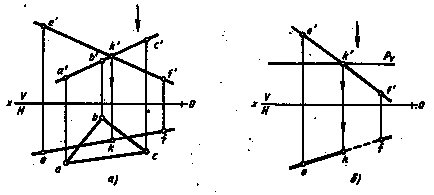
Побудова лінії перетину двох площин зводиться до знаходження двох точок, спільних для цих двох площин. Для побудови лінії перетину цього достатньо, так як лінія перетину - пряма, а пряма задається двома точками. При перетині проецирующей площині з площиною загального положення одна з проекцій лінії перетину збігається зі слідом площини, які знаходяться в тій площині проекцій, до якої перпендикулярна проектує площину. На рис. 225, а фронтальна проекція m'n 'лінії перетину MN збігається зі слідом Pv фронтально-проектує площині Р, а на рис. 225, б горизонтальна проекція kl збігається зі слідом горизонтально-проецирующей площині R. Інші проекції лінії перетину будуються за допомогою ліній проекційної зв'язку.
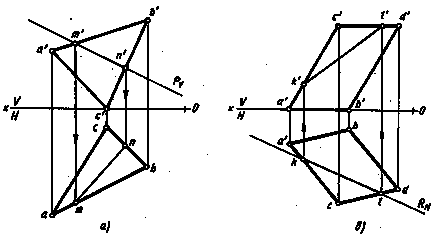
Побудова точки перетину прямої з площиною загального положення (рис. 226, а) виконують за допомогою допоміжної проецирующей площині R, яку проводять через дану пряму EF. Будують лінію перетину 12 допоміжної площини R із заданою площиною трикутника ABC, отримують в площині R дві прямі: EF - задана пряма і 12 - побудована лінія перетину, які перетинаються в точці К.
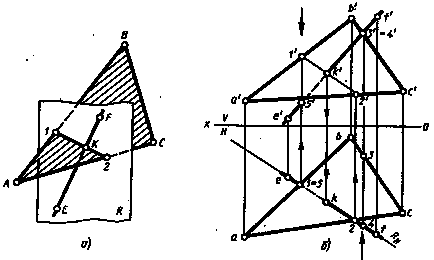
Знаходження проекцій точки К показано на рис. 226, б. Побудови виконують в такій послідовності.
Через пряму EF проводять допоміжну горизонтально-проецирующую площину R. Її слід RH збігається з горизонтальною проекцією ef прямий EF.
Будують фронтальну проекцію 1'2 'лінії перетину 12 площині R із заданою площиною трикутника ABC за допомогою ліній проекційної зв'язку, так як горизонтальна проекція лінії перетину відома. Вона збігається з горизонтальним слідом RH площині R.
Визначають фронтальну проекцію k 'шуканої точки К, яка знаходиться в перетині фронтальної проекції даної прямої з проекцією 1'2' лінії перетину. Горизонтальна проекція точки будується за допомогою лінії проекційної зв'язку.
Видимість прямий відносно площини трикутника ABC визначається способом конкуруючих точок. Для визначення видимості прямий на фронтальній площині проекцій (рис. 226, б) порівняємо координати Y точок 3 і 4, фронтальні проекції яких збігаються. Координата Y точки 3, що лежить на прямій ВС, менше координати Y точки 4, що лежить на прямій EF. Отже, точка 4 знаходиться ближче до спостерігача (напрямок погляду вказано стрілкою) і проекція прямої зображується на площині V видимою. Пряма проходить перед трикутником. Лівіше точки К 'пряма закрита площиною трикутника ABC.
Видимість на горизонтальній площині проекцій показують, порівнявши координати Z точок 1 і 5. Так як Z1> Z5. точка 1 видима. Отже, правіше точки 1 (до точки К) пряма EF невидима.
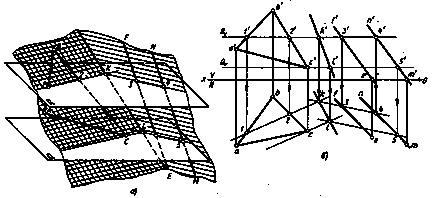
Для побудови лінії перетину двох площин загального положення застосовують допоміжні січні площини. Це показано на рис. 227, а. Одна площину задана трикутником ABC, інша - паралельними прямими EF і MN. Задані площині (рис. 227, а) перетинають третьої допоміжної площиною. Для простоти побудов в якості допоміжних площин беруть горизонтальні або фронтальні площині. В даному випадку допоміжна площина R є горизонтальною площиною. Вона перетинає задані площини за прямими лініями 12 і 34, які в перетині дають точку К, яка належить всім трьом площинам, а отже, і двом заданим, т. Е. Лежить на лінії перетину заданих площин. Другу точку знаходять за допомогою другої допоміжної площини Q. Знайдені дві точки К і L визначають лінію перетину двох площин.
На рис. 227, б допоміжна площина R задана фронтальним слідом. Фронтальні проекції ліній перетину 1'2 'і 3'4 площині R з заданими площинами збігаються з фронтальним слідом Rv площині R, так як площину R перпендикулярна площині V, і все, що в ній знаходиться (в тому числі і лінії перетину) проектується на її фронтальний слід Rv. Горизонтальні проекції цих ліній побудовані за допомогою ліній проекційної зв'язку, проведених від фронтальних проекцій точок 1 ', 2', 3 ', 4' до перетину з горизонтальними проекціями відповідних прямих в точках 1, 2, 3, 4. Побудовані горизонтальні проекції ліній перетину продовжують до перетину один з одним в точці k, яка є горизонтальною проекцією точки К, що належить лінії перетину двох площин. Фронтальна проекція цієї точки знаходиться на сліді Rv.
Для побудови другої точки, що належить лінії перетину, проводять другу допоміжну площину Q. Для зручності побудов площину Q проведена через точку С паралельно площині R. Тоді для побудови горизонтальних проекцій ліній перетину площини Q з площиною трикутника АВС і з площиною, заданої паралельними прямими, досить знайти дві точки: з і 5 і провести через них прямі, паралельні раніше побудованим проекція ліній перетину 12 і 34, так як площину Q ║ R. Продовживши ці прямі до перетину один з друг м, отримують горизонтальну проекцію l точки L, що належить лінії перетину заданих площин. Фронтальна проекція l 'точки L лежить на сліді Qv і будується за допомогою лінії проекційної зв'язку. Поєднавши однойменні проекції точок К і L, отримують проекції шуканої лінії перетину.
Якщо в одній з пересічних площин взяти пряму і побудувати точку перетину цієї прямої з іншого площиною, то ця точка буде належати лінії перетину цих площин, так як вона належить обом заданим площинах. Побудуємо таким же чином другу точку, можна знайти лінію перетину двох площин, так як для побудови прямої достатньо двох точок. На рис. 228 показано таке побудова лінії перетину двох площин, заданих трикутниками.
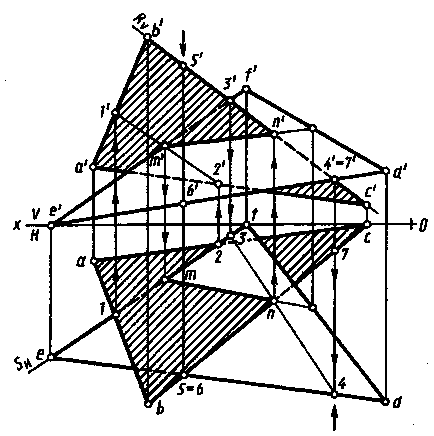
Для даного побудови беруть одну зі сторін трикутника і будують точку перетину цієї сторони з площиною іншого трикутника. Якщо це не вдається, беруть іншу сторону цього ж трикутника, потім третю. Якщо і це не привело до знаходження шуканої точки, будують точки перетину сторін другого трикутника з першим.
На рис. 228 побудована точка перетину прямої EF з площиною трикутника ABC. Для цього через пряму EF проводять допоміжну горизонтально-проецирующую площину S і будують фронтальну проекцію 1'2 'лінії перетину цієї площини з площиною трикутника АВС. Фронтальна проекція 1'2 'лінії перетину, перетинаючись з фронтальною проекцією e'f' прямий EF, дає фронтальну проекцію m 'точки перетину М. Горизонтальну проекцію m точки М знаходять за допомогою лінії проекційної зв'язку. Друга точка, що належить лінії перетину площин заданих трикутників, - точка N - точка перетину прямої ВС з площиною трикутника DEF. Через пряму ВС проводять фронтально-проецирующую площину R, і на площині H перетин горизонтальних проекцій прямої ВС і лінії перетину 34 дає точку n - горизонтальну проекцію шуканої точки. Фронтальна проекція побудована за допомогою лінії проекційної зв'язку. Видимі ділянки заданих трикутників визначають за допомогою конкуруючих точок для кожної площині проекцій окремо. Для цього вибирають точку на одній з площин проекцій, яка є проекцією двох конкуруючих точок. За другим проекція цих точок визначають видимість, порівнюючи їх координати.
Наприклад, точки 5 і 6 - точки перетину горизонтальних проекцій bc і de. На фронтальній площині проекцій проекції цих точок не збігаються. Порівнявши їх координати Z, з'ясовують, що точка 5 закриває точку 6, так як координата Z5. більше координати Z6. Отже, лівіше точки 5 сторона DE невидима.
Видимість на фронтальній площині проекцій визначаю за допомогою конкуруючих точок 4 і 7, що належать відрізкам DE і ВС, порівнюючи їх координати Y4 і Y7 Так як Y4> Y7. сторона DE на площині V видима.
Слід зазначити, що при побудові точки перетину прямої з площиною трикутника точка перетину може виявитися за межами площини трикутника. В цьому випадку, з'єднавши отримані точки, що належать лінії перетину, обводять тільки той її ділянку, що належить обом трикутниках.
ПИТАННЯ ДЛЯ ПОВТОРЕННЯ
1. Які координати точки визначають її положення в площині V?
2. Що визначають координата Y і координата Z точки?
3. Як розташовуються на епюрі проекції відрізка, перпендикулярного площині проекцій Н? Перпендикулярного площині проекцій V?
4. Як розташовуються на епюрі проекції горизонталі, фронталі?
5. Сформулюйте основне положення про приналежність точки прямої.
6. Як відрізнити на епюрі пересічні прямі від перехресних?
7. Які точки називають конкуруючими?
8. Як визначити, яка з двох точок видима, якщо їх проекції на фронтальній площині проекцій збіглися?
9. Сформулюйте основне положення про паралельність прямої і площини.
10. Який порядок побудови точки перетину прямої з площиною загального положення?
11. Який порядок побудові лінії перетину двох площин загального положення?