Перетин прямої з площиною
Якщо пряма не лежить в площині і не паралельна їй, вона перетинає площину.
Завдання на визначення точки перетину прямої з площиною зводиться до наступного:
1) проведення допоміжної площини (Допоміжну площину рекомендується вибирати таку, яка дасть найбільш просте графічне рішення задачі) через дану пряму;
2) знаходження лінії перетину допоміжної площини з даної площиною;
3) визначення точки перетину даної прямої з лінією перетину площин, а отже, з цією площиною.
Перетин прямої з проектує площиною.
Приклад 1. На (фіг.250, а) дані площину δ (δ1) і пряма АВ (А1 В1 і А2 В2); потрібно визначити точку їх перетину.
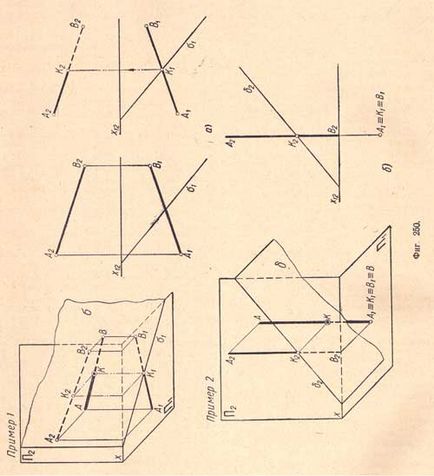
У цьому випадку немає потреби вдаватися до допоміжної площини, так як дана площину δ - горизонтально - проектує. По властивості проектують площин горизонтальна проекція точки перетину, що у площині δ. зливається з горизонтальною проекцією δ1.
Тому точка К1 перетину горизонтальної проекції А1 В1 прямий АВ з горизонтальною проекцією δ1 є горизонтальна проекція точки перетину К; фронтальна проекція К2 визначається шляхом проведення вертикальної лінії зв'язку до перетину її з фронтальною проекцією А2 В2.
Приклад 2. На (фіг.250, б) наведено приклад перетину прямої АВ з фронтально - проектує площиною δ.
Перетин прямої з площиною загального положення.
Приклад 1. Дано: площину загального положення а й пряма загального положення АВ (А1 В1 А2 В2); потрібно знайти точку їх перетину (фіг.251, а).
Проводимо через пряму АВ будь - яку допоміжну площину, наприклад горизонтально - проектує площину δ (δ1), як показано на (фіг.251, б); вона перетне площину a по прямій NM (N1 M1. N2 М2), яка, в свою чергу, перетне пряму АВ (А1 В1 А2 В2) в точці С (С1 С2), що видно на (фіг.251, в). Точка С є точка перетину прямої АВ з площиною а.
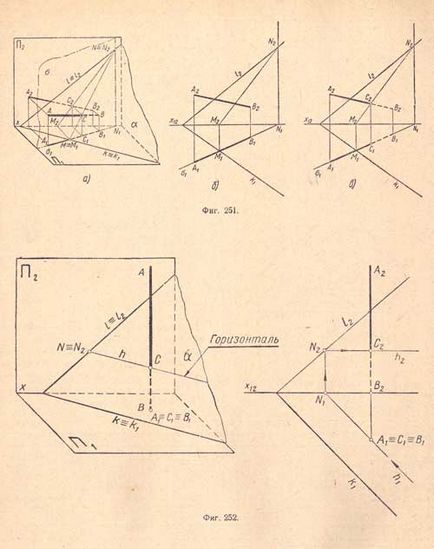
Приклад 2. На (фіг.252) наведено приклад знаходження проекцій точки перетину прямої AB c площиною загального положення за допомогою горизонталі h.
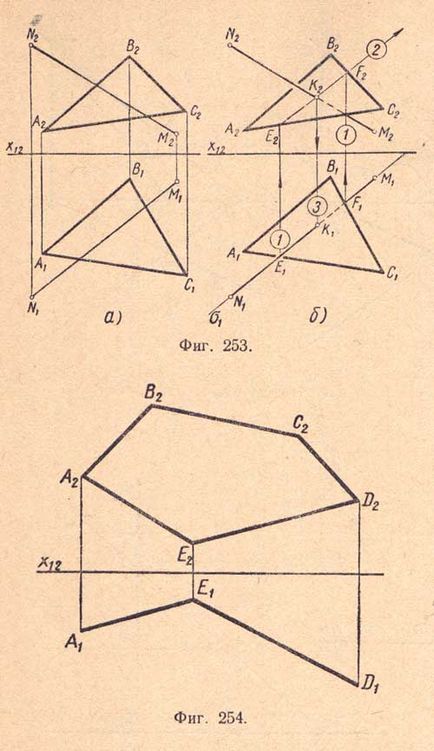
Приклад 3. Дано: трикутник ABC і пряма NM; потрібно визначити точку їх перетину (фіг.253, а).
Візьмемо в якості допоміжної площини горизонтально - проектує площину δ. тоді горизонтальна проекція ог зіллється з горизонтальною проекцією N1 M1 прямий NM і перетне проекції сторін трикутника в точках Е1 і F1 (фіг.253, б). Відрізок Е1 F1 буде горизонтальною проекцією лінії перетину. Потім знаходимо фронтальну проекцію лінії перетину: за допомогою вертикальних ліній зв'язку отримуємо точки Е2 і F2. проводимо через них пряму E2 F2. яка буде фронтальною проекцією лінії перетину.
Пряма E2 F2 перетинає пряму N2 М2 в точці К2. Точка К2 буде фронтальною проекцією точки перетину прямої MN з прямою EF; горизонтальну проекцію K1 цієї точки визначаємо за допомогою вертикальної лінії зв'язку.
Точка К (K1. К2) буде точкою перетину даної прямої MN з даними трикутником ABC. як одночасно їм належить, тому що пряма MN перетинається в ній з прямою EF. лежить в площині трикутника ABC.
Вправа 1
Побудувати комплексне креслення трикутника ABC за даними координатами вершин. Знайти натуральну величину сторін трикутника і побудувати його в натуральну величину. За цим же координатах побудувати наочне зображення
Вправа 2
За даними фронтальної проекції багатокутника і горизонтальним проекція двох суміжних сторін його добудувати горизонтальну проекцію багатокутника.
У площині багатокутника побудувати проекції довільного трикутника. Побудувати точку поза багатокутника, але що лежить в одній площині з ним (фіг.254)