Перетин прямої і площини в нарисної геометрії
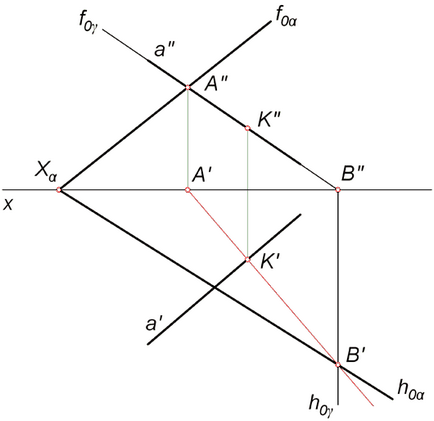
Відомо, що пряма перетинає площину, якщо вона не належить цій площині і не паралельна їй. Дотримуючись наведеним нижче алгоритмом, знайдемо точку перетину прямої a з площиною загального положення α, заданої слідами h0α. f0α.
- Через пряму a проводимо допоміжну фронтально-проецирующую площину γ. На малюнку позначені її сліди h0γ. f0γ.
- Будуємо проекції прямої AB, по якій перетинаються площини α і γ. У цьому завданню точка B '= h0α ∩ h0γ. A '' = f0α ∩ f0γ. Точки A 'і B' 'лежать на осі x, їх положення визначається по лініях зв'язку.
- Прямі a і AB перетинаються в шуканої точці K. Її горизонтальна проекція K '= a' ∩ A'B '. Фронтальна проекція K '' лежить на прямій a ''.
Алгоритм рішення залишиться тим же, якщо пл. α буде задана паралельними, перехресними прямими, відсіком фігури або іншими можливими способами.
Видимість прямий a відносно площини α. Метод конкуруючих точок
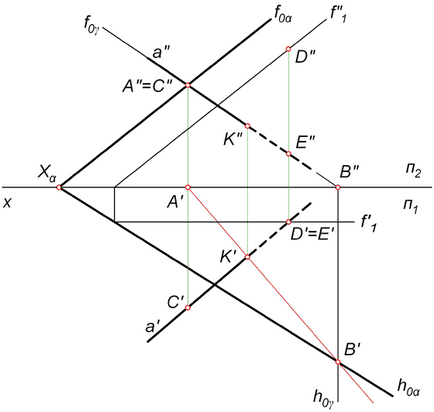
- Відзначимо на кресленні фронтально-конкуруючі точки A і С (рис. Нижче). Будемо вважати, що точка A належить пл. α, а З лежить на прямій a. Фронтальні проекції A '' і С '' збігаються, але при цьому т. A і С віддалені від площини проекцій П2 на різну відстань.
- Знайдемо горизонтальні проекції A 'і C'. Як видно на малюнку, точка C 'віддалена від площини П2 на більшу відстань, ніж т. A', що належить пл. α. Отже, ділянка прямої а '', розташований лівіше точки K '', буде видимим. Ділянка a '' правіше K '' є невидимим. Відзначаємо його штриховий лінією.
- Відзначимо на кресленні горизонтально-конкуруючі точки D і E. Вважатимемо, що точка D належить пл. α, а E лежить на прямій a. Горизонтальні проекції D 'і E' збігаються, але при цьому т. D і E віддалені від площини П1 на різну відстань.
- Визначимо положення фронтальних проекцій D '' і E ''. Як видно на малюнку, точка D '', що знаходиться в пл. α, віддалена від площини П1 на більшу відстань, ніж т. E '', що належить прямій a. Отже, ділянка а ', розташований правіше точки K', буде невидимим. Відзначаємо його штриховий лінією. Ділянка a 'лівіше K' є видимим.