Основні правила диференціювання і похідні елементарних функцій

Загальне правило диференціювання. При диференціюванні функції (знаходження її похідної) дотримуються наступні схеми:

вибравши деяке значення х. дають йому пріращеніех і знаходять значення функції в точкех + х. равноеf (x + x);

складають відношення f / x і, якщо можливо, спрощують його;

знаходять похідну функції, тобто межа

(f / x). якщо ця межа існує:

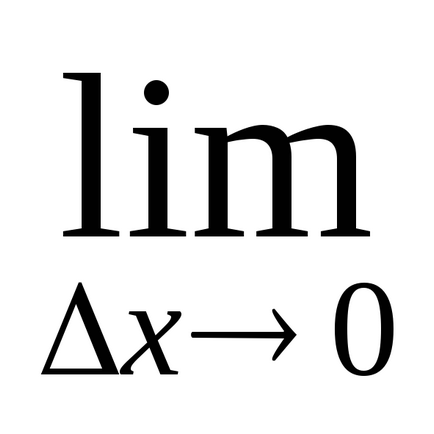
Похідна алгебраїчній суми диференційовних функцій дорівнює алгебраїчній сумі похідних цих функцій.

Похідна добутку двох диференційовних функцій дорівнює сумі творів другої функції на похідну першої і першої функції на похідну другої:

Похідна приватного (дробу) двох функцій дорівнює дробу, знаменник якого дорівнює квадрату знаменника диференціюється, а чисельник є різниця між творами знаменника на похідну чисельника і чисельника на похідну знаменника:

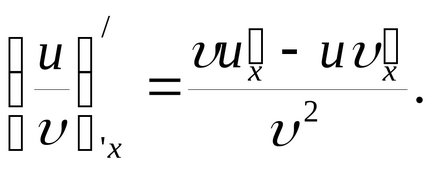
ПОХІДНА СКЛАДНОЇ ФУНКЦІЇ.

Будь-яку складну функцію можна представити у вигляді елементарних функцій, які є її проміжними аргументами.

Схожі статті

• Основні правила диференціювання - студопедія

• Основні правила диференціювання

• Основні функції президента рф