Оцінки як випадкові величини одержувана оцінка являє окремий випадок випадкової змінної
Отримана оцінка являє окремий випадок випадкової змінної. Причина тут в тому, що поєднання значень х в вибірці випадково, оскільки х - випадкова змінна і, отже, випадковою величиною є і голосовий набір її значень. Візьмемо, наприклад, х - оцінку математичного очікування:
; = + * 2 (021)
Ми тільки що показали, що величинах в / -м спостереженні може бути розкладена на дві складові: постійну частину р і чисто випадкову складову Uf
х, = р + иг (0.22)
отже,
х = р + і, (0.23)
де й - вибіркове середнє величин і.
Звідси можна бачити, що х, подібно х, має як фіксовану, так і чисто випадкову складові. Її фіксована складова - р, тобто математичне очікування х, а її випадкова складова - і, тобто середнє значення чисто випадкової складової в вибірці.
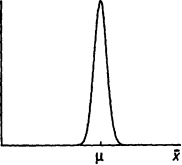
Функції щільності ймовірності для х і х показані на однакових графіках (рис. 0.7). Як показано на малюнку, величина х вважається нормально розподіленою. Можна бачити, що розподілу, як х, так і х, симетричні щодо р - теоретичного середнього. Різниця між ними в тому, що
розподіл х ^ ж і вище. Величина х, ймовірно, повинна бути ближче до р,
ніж значення одиничного спостереження х, оскільки її випадкова складова і є середнє від чисто випадкових складових їх, і 2. ип в вибірці, які, мабуть, «гасять» один одного при розрахунку середнього.
Далі, теоретична дисперсія величини і становить лише частина теоретичної дисперсії і. У розділі 1.7 буде засвідчили, що якщо pop. var (і) = А2, то pop. var (і) = А2 / л.
Функція щільності Функція щільності
ймовірності х ймовірності X
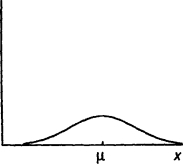
Мал. 0.7. Порівняння функцій щільності ймовірності одиночного спостереження
і вибіркового середнього
Величина j 2 - оцінка теоретичної дисперсії х - також є випадковою змінною. Віднімаючи (0.23) з (0.22), маємо:
xi-x = uj-u. (0.24)
отже,
* 2 = ^ їі = - ^ їі. (0.25)
Таким чином, s2 залежить від (і тільки від) чисто випадкової складової спостережень х у вибірці. Оскільки ці складові змінюються від вибірки до вибірки, також від вибірки до вибірки змінюється і величина оцінки s2.