Оцінки як випадкові величини, безкоштовні курсові, реферати, дипломні роботи
Отримана оцінка являє окремий випадок випадкової змінної. Причина тут в тому, що поєднання значень у вибірці випадково, оскільки - випадкова змінна і, отже, випадковою величиною є і голосовий набір її значень. Візьмемо, наприклад, - оцінку математичного очікування:
Вище ми показали, що величина в -м спостереженні може бути розкладена на дві складові: постійну частину і чисто випадкову складову:
де - вибіркове середнє величин.
Звідси можна бачити, що, ...
подібно, має як фіксовану, так і чисто випадкову складові. Її фіксована складова -, тобто математичне сподівання, а її випадкова складова -, тобто середнє значення чисто випадкової складової в вибірці.
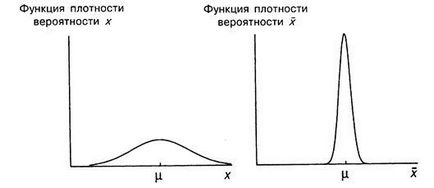
Функції щільності ймовірності для і показані на однакових графіках (рис. A.6). Як показано на малюнку, величина вважається нормально розподіленою. Можна бачити, що розподілу, як, так і, симетричні відносно - теоретичного середнього. Різниця між ними в тому, що розподіл вже і вище. Величина, ймовірно, повинна бути ближче до, ніж значення одиничного спостереження, оскільки її випадкова складова є середнє від чисто випадкових складових у вибірці, які, мабуть, «гасять» один одного при розрахунку середнього. Далі теоретична дисперсія величини становить лише частина теоретичної дисперсії.