Оцінки як випадкові величини
Отримана оцінка являє окремий випадок випадкової змінної. Причина тут в тому, що поєднання значень x у вибірці випадково, оскільки x - випадкова змінна і, отже, випадковою величиною є і голосовий набір її значень. Візьмемо, наприклад, - оцінку математичного очікування:
Вище було показано, що величина x в i-му спостереженні може бути розкладена на дві складові: постійну частину і чисто випадкову складову:
де - вибіркове середнє величин.
Звідси можна бачити, що. подібно x. має як фіксовану, так і чисто випадкову складові. Її фіксована складова -. тобто математичне очікування x. а її випадкова складова -. тобто середнє значення чисто випадкової складової в вибірці.
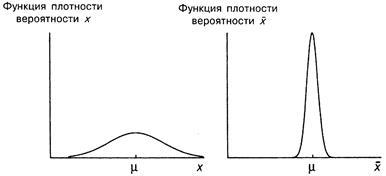
Функції щільності ймовірності для x і показані на однакових графіках (рис. 6). Величина x вважається нормально розподіленою. Можна бачити, що розподілу, як x. так і . симетричні відносно - теоретичного середнього. Різниця між ними в тому, що розподіл вже і вище. Величина. ймовірно, повинна бути ближче до. ніж значення одиничного спостереження x. оскільки її випадкова складова є середнє від чисто випадкових складових у вибірці, які, мабуть, «гасять» один одного при розрахунку середнього. Далі теоретична дисперсія величини становить лише частина теоретичної дисперсії.
Величина - оцінка теоретичної дисперсії x - також є випадковою змінною. Віднімаючи (18) з (17), маємо:
Таким чином, залежить тільки від чисто випадкової складової спостережень x в вибірці. Оскільки ці складові змінюються від вибірки до вибірки, також від вибірки до вибірки змінюється і величина оцінки.
Оскільки оцінки є випадковими змінними, їх значення лише за випадковим збігом можуть в точності дорівнювати характеристикам генеральної сукупності. Зазвичай буде присутній певна помилка, яка може бути великий чи малої, позитивною або негативною, в залежності від чисто випадкових складових величин x в вибірці.
Хоча це і неминуче, на інтуїтивному рівні бажано, проте, щоб оцінка в середньому за досить тривалий період була акуратною. Висловлюючись формально, ми хотіли б, щоб математичне сподівання оцінки дорівнювало б відповідної характеристиці генеральної сукупності. Якщо це так, то оцінка називається несмещенной. Якщо це не так, то оцінка називається зміщеною. і різниця між її математичним очікуванням і відповідної теоретичної характеристикою генеральної сукупності називається зміщенням.
Почнемо з вибіркового середнього. Чи є воно несмещенной оцінкою теоретичного середнього? Чи рівні і. Так, це так, що безпосередньо випливає з (18).
Величина x включає дві складові - і. Значення дорівнює середній чисто випадкових складових величин x в вибірці, і, оскільки математичне очікування такої складової в кожному спостереженні дорівнює нулю, математичне сподівання дорівнює нулю. отже,
Проте, отримана оцінка - не єдино можлива несмещенная оцінка. Припустимо для простоти, що у нас є вибірка всього з двох спостережень - і. Будь-яке зважене середнє спостережень і було б несмещенной оцінкою, якщо сума ваг дорівнює одиниці. Щоб показати це, припустимо, що ми побудували узагальнену формулу оцінки:
Математичне сподівання Z одно:
Якщо сума і дорівнює одиниці, то ми маємо і Z є несмещенной оцінкою.
Таким чином, в принципі число незміщене оцінок нескінченно. Як вибрати одну з них? Чому насправді ми завжди використовуємо вибіркове середнє з?
До сих пір ми розглядали тільки оцінки теоретичного середнього. Вище стверджувалося, що величина. визначається відповідно до табл. 6, є оцінкою теоретичної дисперсії. Можна показати, що математичне сподівання дорівнює. і ця величина є несмещенной оцінкою теоретичної дисперсії, якщо спостереження у вибірці незалежні один від одного. Доказ цього математично нескладно, але занадто багато роботи, і тому ми його опускаємо.
Незміщеність - бажане властивість оцінок, але це не єдина така властивість. Ще одна важлива їх сторона - це надійність. Звичайно, важливо, щоб оцінка була точною в середньому за тривалий період. Ми хотіли б, щоб наша оцінка з максимально можливою вірогідністю давала б близьке значення до теоретичної характеристиці, що означає бажання отримати функцію щільності ймовірності, як можна більш «стислу» навколо істинного значення. Один із способів висловити цю вимогу - сказати, що ми хотіли б отримати наскільки можливо малу дисперсію.
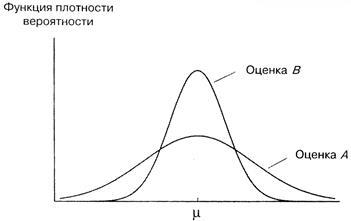
Припустимо, що ми маємо дві оцінки теоретичного середнього, розраховані на основі однієї і тієї ж інформації, що обидві вони є незміщеними і що їх функції щільності ймовірності показані на рис. 7. Оскільки функція щільності ймовірності для оцінки B більш «стиснута», ніж для оцінки A. з її допомогою ми швидше отримаємо більш точне значення. Формально кажучи, ця оцінка більш ефективна.
Ми говорили про бажання отримати оцінку як можна з меншою дисперсією, і ефективна оцінка - це та, у якій дисперсія мінімальна. Зараз ми розглянемо дисперсію узагальненої оцінки теоретичного середнього і покажемо, що вона мінімальна в тому випадку, коли обидва спостереження мають рівні ваги.
Якщо спостереження і незалежні, теоретична дисперсія узагальненої оцінки дорівнює:
Ми вже з'ясували, що для незсуненості оцінки необхідно рівність одиниці суми і. Отже, для незміщене оцінок і
Оскільки ми хочемо вибрати так, щоб мінімізувати дисперсію, нам потрібно мінімізувати при цьому. Це завдання можна вирішити графічно або за допомогою диференціального обчислення. У будь-якому випадку мінімум досягається при. Отже, також дорівнює 0,5.
Отже, ми показали, що вибіркове середнє має найменшу дисперсію серед оцінок розглянутого типу. Це означає, що вона має більш «стислий» імовірнісний розподіл навколо істинного середнього і, отже (в імовірнісному сенсі), найбільш точно. Строго кажучи, вибіркове середнє - це найбільш ефективна оцінка серед усіх незміщене оцінок. Звичайно, ми показали це тільки для випадку з двома спостереженнями, але зроблені висновки вірні для вибірок будь-якого розміру, якщо спостереження не залежать один від одного.
Два зауваження: по-перше, ефективність оцінок можна порівнювати лише тоді, коли вони використовують одну і ту ж інформацію, наприклад один і той же набір спостережень декількох випадкових змінних. Якщо одна з оцінок використовує в 10 разів більше інформації, ніж інша, то вона цілком може мати меншу дисперсію, але було б неправильно вважати її більш ефективною. По-друге, ми обмежуємо поняття ефективності порівнянням розподілів незміщене оцінок. Існують визначення ефективності, узагальнюючі це поняття на випадок можливого порівняння зміщених оцінок.