Момент сили і момент імпульсу - студопедія
Обертання є складовою більшості розглянутих в механіці рухів. Кожен день ми є свідками великого космічного обертання. Дані останніх теоретичних досліджень говорять, що все навколо і ми самі за властивостями нагадуємо що обертаються з великою частотою поля.
Динамічні характеристики - момент сили і момент імпульсу. використовувані при описі обертального руху, грають в теорії обертального руху таку ж велику роль. як ую сила і імпульс грають в динаміці поступального руху.
Відомо, що пересунути масивний предмет (наприклад, ящик) вручну важко, набагато легше пересунути його за допомогою довгої палиці, труби (брухту), тобто перекантувати за допомогою важеля, причому, чим довший цей важіль, тим легше це зробити (прикладається менша сила при більшій довжині важеля (див. рис. 4.8)). Згадаймо знаменитий вислів Архімеда (бл. 286-212 рр. До н.е.). «Дайте мені точку опори (і важіль) і я переверну Землю».
Інший приклад - зважування предметів на вагах (див. Рис. 4.9): при рівних плечах (сили) ваг li переважить той вантаж, маса якого mi більше, а якщо маси вантажів рівні, то переважить вантаж, для якого плече сили li більше.
Слід розрізняти момент сили і момент імпульсу відносно точки і відносно осі, в першому випадку - це вектора, а в другому - проекції векторів (скаляри).
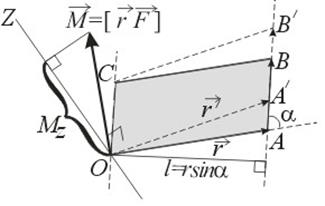
Нехай дана точка О (полюс), щодо якої знаходиться момент сили. Моментом сили відносно точки О називається векторний добуток (вектор) радіуса-вектора. проведеного з точки О в точку А прикладання сили на вектор:
Модуль моменту сили:
де l = rsina - найкоротша відстань до лінії АВ дії сили (рис.4.10), зване плече м сили l.
При цьому вектор не зміниться, якщо точку прикладання сили перенести в будь-яку іншу точку, розташовану на лінії дії сили. наприклад в точку А /. При цьому паралелограм ОАВС перейде в паралелограм ОА / В / С. Обидва паралелограма мають однакові підстава і висоту, а отже, і площа.
На відміну від полярних векторів (саме їх вивчають в школі), вектора, що характеризують обертальний рух. не мають конкретної точки прикладання (див. також лекція 1, п.1), їх називають легкими. Так, вектор можна відкладати від будь-якої точки паралельно одному з напрямків, отриманого в результаті векторного твори (за властивостями векторного твори перпендикулярно площині, в якій лежать два перемножуєте вектора -), напрямок вектора збігається з напрямком поступального руху правого гвинта при його обертанні від вектора до (в математиці термін - «ліва трійка»).
Головним моментомнесколькіх зовнішніх сил, що діють на систему, щодо точки Оназивается сума моментів їх щодо цієї точки (принцип незалежності дії сил):
де сили вважають прикладеними до однієї точки О. що можна отримати шляхом паралельного перенесення векторів (часто в механіці для зручності при вирішенні задач сили розглядають як прикладені до центру мас тіла, хоча це не для всіх сил так, приклад - сила тертя прикладена до поверхні тіла ).
При обертанні ТТ (системи матеріальних точок) необхідно враховувати тільки зовнішні сили, так як внутрішні сили взаємодії двох будь-яких елементів ТТ (системи) завжди рівні за модулем (величиною) і протівонаправлени уздовж однієї прямої (їх векторна (геометрична) сума дорівнює нулю).
Аналогічно вищесказаного можна визначити момент імпульсу відносно точки (вектор) і відносно осі (проекція вектора Lz):
де - імпульс (матеріальної) точки А.. Важливо відзначити, що моментом імпульсу відносно точки може володіти і тіло, що рухається поступально (достатня наявність імпульсу і плеча). Тіло, що володіє імпульсом, може не мати моментом імпульсу щодо одних точок (за відсутності плеча) і мати відносно інших.
Одиниці виміру [М] = Н × м (не плутати з [А] = Дж = Н × м), а.
У загальному випадку (неколінеарна) і. тобто і. але якщо полюс (точка) Про нерухомий, то імпульс точки А сонаправлени з її швидкістю. тоді:
тобто отримують основне рівняння динаміки обертального руху:
Цей закон залишається справедливим і для системи матеріальних точок, в цьому випадку
Особливість обертання ТТ, в порівнянні з системою непов'язаних один з одним матеріальних точок, полягає в тому, що при обертанні ТТ навколо нерухомої осі всі його елементи рухаються по колах, причому кутова швидкість обертання для них однакова (а лінійна різна). Тому природним буде висловити вектор через швидкість.
Розіб'ємо ТТ (рис. 4.11), що обертається щодо осі ОО /. на елементи (матеріальні точки). Момент імпульсу кожного елемента
З урахуванням рівності
В математиці відомо, що подвійний векторний добуток має вигляд
де DIi - момент інерції i -го елемента.
Підсумовуючи (інтегруючи) по всіх елементах, отримують:
З урахуванням формул (4.20) і (4.23) отримуємо ще одну форму записи основного рівняння динаміки обертального руху:
де e - кутове прискорення.
При обертанні ТТ (системи матеріальних точок) необхідно враховувати тільки зовнішні сили, так як внутрішні сили взаємодії двох будь-яких елементів ТТ (системи) завжди рівні за модулем (величиною) і протівонаправлени уздовж однієї прямої (їх векторна (геометрична) сума дорівнює нулю). Відповідно до рівняння (4.21) для замкнутої системи маємо:
Значить, для замкнутих систем виконується закон збереження моменту імпульсу.