Методика математики
- Ознайомити учнів з геометричними тілами - кулею, конусом, циліндром і їх елементами.
- Навчити розрізняти в навколишньому світі предмети, що мають форму досліджуваних фігур.
- Вміти оперувати поняттями: куля, конус, циліндр, багатогранник, тіло обертання, поверхня тіла, розтин.
- Вміти розпізнавати вивчені геометричні фігури.
- Вміти наводити приклади предметів, що мають форму вивчених тіл обертання.
- Вміти розповідати про кулі, конуса, циліндрі за планом.
- Організаційний момент.
- Актуалізація знань.
- Вивчення циліндра.
- Вивчення конуса.
- Вивчення кулі.
- Багатогранники і тіла обертання.
- Вирішення задач.
- Підбиття підсумку уроку.
- Домашнє завдання.
- Креслярські інструменти.
- Ребуси.
- Малюнки до завдань.
... На сьогоднішньому уроці ви познайомитеся з трьома новими геометричними фігурами. Щоб краще зрозуміти досліджуваний матеріал будьте уважними, активними і кмітливими.
Тема уроку складається з трьох слів, які зашифровані за допомогою ребусів. Розгадати їх і ви дізнаєтеся які геометричні фігури ми будемо вивчати сьогодні.


Отже, тема уроку "Куля. Конус. Циліндр".
Перш ніж почнемо знайомитися з новими геометричними фігурами, дайте відповідь на кілька питань.
- Яка фігура, на вашу думку, є зайвою і чому? Можливі кілька варіантів відповідей!
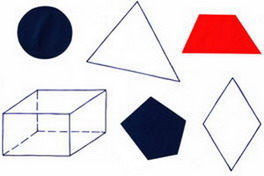
зайва, тому що кругла;
зайва, тому що червона;
зайва, тому що об'ємні.
Хочу зауважити, що на уроках математики не має значення колір предмета і матеріал, з якого він виготовлений. Важлива форма і розміри досліджуваної фігури. За однією із запропонованих вами класифікацій зайвим є прямокутний паралелепіпед, так як він є просторовою фігурою, а решту фігур плоскі.
- Які ще просторові фігури ви знаєте?
куб, паралелепіпед, піраміда.
Основні елементи піраміди повторили, а тепер згадаємо важливі моменти, пов'язані з прямокутним параллелепипедом і кубом. Для цього вирішимо дві задачі.
Знайдіть об'єм акваріума, зображеного на малюнку.
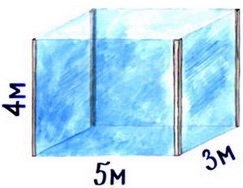
Від куба відрізали кут. Скільки граней у вийшла фігури?
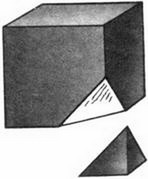
Отже, все раніше вивчені просторові фігури ми згадали, приступимо до вивчення нових фігур, які будемо вивчати за планом, записаному на дошці.
- Походження назви фігури.
- Приклади.
- Поверхня.
- Перетину.
Почнемо з циліндра.
Виявляється, слово "циліндр" походить від грецького слова "кюліндрос", що означає "валик", "каток". На рубежі XVIII - XIX століть чоловіки багатьох країн носили тверді капелюхи з невеликими полями, які так і називалися циліндрами через велику схожість з геометричною фігурою циліндром.
- Які ще предмети мають циліндричну форму?
стакан, олівець, багато баночки,
каструлі, бідони, частина качалки і т.д.

Уважно подивіться на циліндр (демонструється модель). Циліндр, як ми бачимо, просторова або об'ємна фігура. Поверхня циліндра складається з двох підстав і бічної поверхні.
- Що з себе представляють підстави циліндра?
- Що ви можете сказати про розміри цих кіл?
однакові, тобто радіуси цих кіл рівні.
- Що з себе являє бокова поверхня?
Візьмемо паперовий циліндр, разрежем його наступним чином (показую) і розгорнемо.
- Так що ж являє собою бокова поверхня?
Що ще потрібно знати про циліндрі?
Висота циліндра - це відстань між основами, радіус циліндра - радіус кола, що є підставою циліндра.
А зараз уявіть, що у кожного з вас в руках дерев'яний циліндр і топірець, за допомогою якого ви легко можете розсікти або розколоти циліндр. "Обережно" сокиркою вдаряє по верхньому основи і розколюємо його (показую на моделі). Він розпадеться на дві половинки.
- Форму який геометричної фігури має зріз або по науковому кажуть перетин циліндра? Багато, напевно, бачили як колють дрова!
А зараз будемо "пиляти" циліндр, поклавши його "на бік". Подумки його розпиляємо або рассечём.
- Яка геометрична фігура вийде на зрізі або говорять в перерізі циліндра?
Продовжуємо працювати далі, знову покладемо циліндр на бічну поверхню, але рассечём його вже "навскоси".
- Яка геометрична фігура буде в перерізі, тобто на зрізі?
Овал, по-науковому, еліпс (заздалегідь записати на центральній дошці під циліндром).
- Отже, які геометричні фігури можуть бути в перерізі циліндра?
прямокутник, коло, еліпс.
Всі пункти плану розібрані, ви вже досить багато знаєте про циліндрі. Переходимо до розгляду конуса.
Слово "конус" походить від грецького слова "Коносу", що означає соснову шишку (показую шишку). Дійсно, є певна схожість.
Конус, як і циліндр, є просторовою фігурою. Поверхня конуса складається з кола, який називається підставою конуса і бічній поверхні.
- Що ж із себе представляє бокова поверхня?
Важко подумки уявити бічну поверхню конуса, тому, як і в випадку з циліндром, візьмемо паперовий конус, разрежем його наступним чином (показую) і розгорнемо.
- Що є розгорткою бічної поверхні конуса? Що це таке? Частиною який геометричної фігури є ця фігура?
Конус, на відміну від циліндра, має вершину (показую вершину, висоту і радіус підстави по малюнку на центральній дошці).
Якщо вершину і верхню частину конуса відсікти (показую на моделі). то ми отримаємо так званий усічений конус.
відро, горщики для квітів,
воронка, морозиво-ріжок і ін.
А зараз знову уявімо, що ми розсікає дерев'яний конус.
- Форми яких геометричних фігур можуть мати перетину конуса?
трикутника, кола, еліпса.
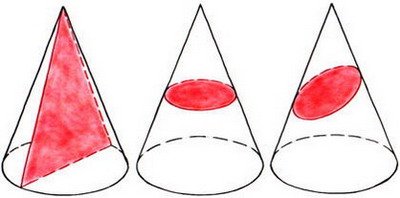
Виявляється, перетину конуса можуть мати форми інших геометричних фігур, назви яких ми навіть ще не знаємо, їх будемо вивчати в старших класах, і тому про них поки говорити не будемо.
Знову всі пункти плану нами розглянуті.
І, нарешті, переходимо до вивчення кулі.
Куля - це найбільш знайома вам геометрична фігура. М'яч (показую) - приклад предмета кулястої форми.
- Які ще предмети мають форму кулі? Хлопці, кому я зараз кину цей м'яч, потрібно привести свій приклад предмета, що має форму кулі.
Виявляється, що куля дуже знайома, але абсолютно не вивчена фігура. Щоб більше дізнатися про кулі, відкрийте підручник на сторінці 137 і самостійно прочитайте пункт 25.
Бачу, що все вже встигли прочитати пункт 25.
Зараз про кулі нам розповість ...
Причому він (вона) розповість більше, ніж написано в підручнику, тому слухайте уважно!
Куля - це просторова фігура. Поверхня кулі називають сферою.
Слово "сфера" походить від грецького слова "сфайра", яке перекладається на українську мову як "м'яч".
Не потрібно плутати поняття "куля" і "сфера". Сфера - це, можна сказати, оболонка або межа кулі.
М'яч, глобус - це сфери, а ось кавун, апельсин, Сонце, Місяць, Земля і інші планети мають форму трохи сплющенного кулі (показує малюнок).

Сфера володіє дуже цікавою властивістю - все її точки однаково віддалені від центру кулі.
Відрізок, що з'єднує будь-яку точку сфери з центром кулі, називається радіусом кулі. На малюнку відрізки ОА, ОВ, ОD і ОС є радіусами (показує по малюнку).
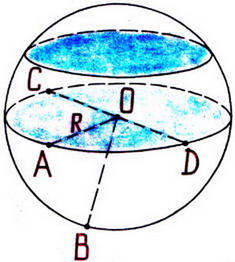
Відрізок, що з'єднує дві точки сфери і проходить через центр кулі, називається діаметром кулі. На малюнку відрізок СD є діаметром кулі. Діаметр кулі дорівнює двом радіусів.
Будь-яке перетин кулі має вигляд кола. Якщо розсікати куля ближче до центру, то кола будуть більше, якщо далі від центру, то радіуси кіл будуть менше.
Отже, ми познайомилися з трьома просторовими геометричними фігурами - кулею, циліндром і конусом. Ви повинні знати, що просторові геометричні фігури ще по-іншому називають геометричними тілами. Виявляється, все геометричні тіла математики роздягли на дві групи: так звані багатогранники і так звані тіла обертання.
Уважно подивіться на геометричні тіла (показую моделі) і спробуйте здогадатися, яке геометричне тіло належить до якої групи.
- Як називається фігура, і до якої групи її віднесемо?
Дійсно, куля, циліндр, конус, усічений конус - тіла обертання. А куб, паралелепіпед, піраміда - багатогранники.
- Чому куб, паралелепіпед, піраміду ви віднесли до многогранників?
Логічно! А ось чому куля, циліндр, конус, усічений конус назвали тілами обертання, про це я вам розповім сама.
Справа тут ось в чому! Якщо взяти плоску фігуру коло або навіть досить половину кола (півколо) і обертати його навколо діаметра, то в повітрі він опише куля. Значить, куля вийшов в результаті обертання півкола. Ось чому куля є тілом обертання, а пряма, навколо якої виробляли обертання, називається віссю обертання кулі або просто віссю кулі.
- Яка плоска фігура при обертанні опише циліндр?
- Яка пряма буде його віссю?
II ряду - про конусі,
III ряду - про кулю;
на альбомному аркуші намалювати предмети, що мають форму знову вивчених геометричних фігур.
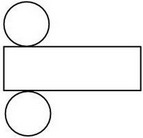
На малюнку 1, а зображений циліндр. Зверху і знизу циліндр обмежений колами, які називаються підставами циліндра. Розгортка бічної поверхні циліндра - прямокутник. На малюнку 1, б зображена розгортка поверхні циліндра. Спробуйте обчислити площу поверхні циліндра, якщо його висота 5 см, а радіус підстав 2 см.
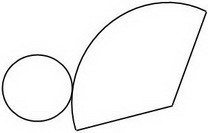
На малюнку 2, а зображений конус. Підстава конуса - коло, а розгортка бічної поверхні - сектор (див. Рис. 2, б). Обчисліть площу поверхні конуса, якщо радіус його основи 3 см, а розгортка бічної поверхні - сектор з прямим кутом, радіус цього сектора 12 см. Чи є в умові завдання зайві дані?
Перші кроки в геометрії.