Методи рішення нелінійних рівнянь
Ключові слова: нелінійні рівняння, прикладна математика, САПР MathCAD, метод Ньютона, кроковий метод, метод дихотомії.
Мета роботи: вивчити методи вирішення нелінійних рівнянь з одним невідомим і апробувати їх у дослідно-експериментальній роботі.
- Проаналізувати спеціальну літературу і вибрати найбільш раціональні способи вирішення нелінійних рівнянь, що дозволяють глибоко вивчити і засвоїти цю тему всім випускникам середньої школи.
- Розробити деякі аспекти методики рішення нелінійних рівнянь із застосуванням ІКТ.
- Вивчити методи вирішення нелінійних рівнянь:
- Метод поділу навпіл
Нехай потрібно вирішити нелінійне рівняння виду рівняння F (x) = 0. Припустимо також, що нам заданий деякий інтервал пошуку [x0, x1]. Потрібно знайти інтервал [а, b] довжиною h, що містить перший корінь рівняння, починаючи з лівої межі інтервалу пошуку.
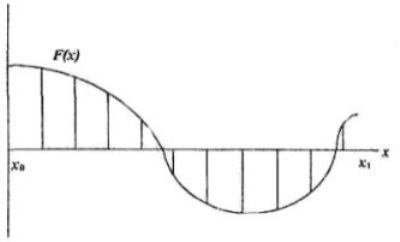
Мал. 1. Кроковий метод
Вирішити це завдання можна декількома способами. Кроковий метод є найбільш простим з чисельних методів розв'язання нерівностей, але для досягнення більшої точності необхідно істотно зменшити крок, а це сильно збільшує час розрахунків. Алгоритм розв'язання рівнянь за допомогою даного методу складається з двох етапів.
На цьому етапі визначаються ділянки, на кожному з яких знаходиться тільки один корінь рівняння. Є кілька варіантів реалізації цього етапу:
- Підставляємо значення X (бажано з якимось досить дрібним кроком) і дивимося де функція змінить знак. Якщо функція змінила знак, це означає, що на ділянці між попереднім і поточним значенням X лежить корінь (якщо функція не змінює характер зростання / спадання, то можна стверджувати, що корінь на цьому інтервалі один).
- Графічний метод. Будуємо графік і оцінюємо на яких інтервалах лежить один корінь.
- Досліджуємо властивості конкретної функції.
На даному етапі значення коренів рівняння, визначених раніше, уточнюється. Як правило на цьому етапі використовуються ітераційні методи. Наприклад, метод половинного ділення (дихотомії) або метод Ньютона.
Метод половинного ділення
Швидкий і досить простий чисельний метод рішення рівнянь, заснований на послідовному звуженні інтервалу, що містить єдиний корінь рівняння F (x) = 0 до того часу, поки не буде досягнута задана точність Е. Даний метод зазвичай використовується при вирішенні квадратних рівнянь і рівнянь вищих ступенів. Однак у даного методу є істотний недолік - якщо на відрізку [а, b] міститься більше одного кореня, то з його допомогою не вдасться домогтися гарних результатів.
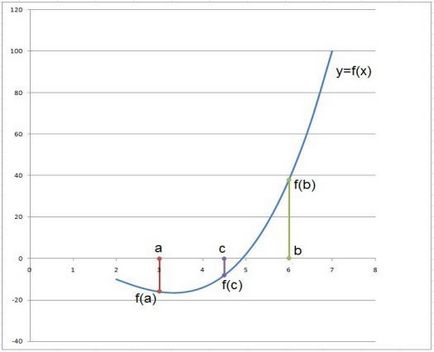
Мал. 2. Метод дихотомії
Алгоритм цього методу наступний:
- Визначити нове наближення кореня х в середині відрізка [а; b]: х = (а + b) / 2.
- Знайти значення функції в точках а і х: F (a) і F (x).
- Перевірити умова F (a) * F (x) 0. Таким чином, вибирається точка з абсцисою x0. в якій дотична до кривої y = f (x) на відрізку [a; b] перетинає вісь Ox. За точку x0 спочатку зручно вибирати один з кінців відрізка.
Погляньмо на цей алгоритм на конкретному прикладі.
Нехай нам дана функція, яка збільшується y = f (x) = x 2 2, безперервна на відрізку (0; 2), і має f '(x) = 2x> 0 і f' '(x) = 2> 0.
У нашому випадку рівняння дотичної має вигляд: y-y0 = 2x0 · (x-x0). В якості точки x0 вибираємо точку B1 (b; f (b)) = (2,2). Проводимо дотичну до функції y = f (x) в точці B1. і позначаємо точку перетину дотичної і осі Ox точкою x1. Отримуємо рівняння першої дотичній: y-2 = 2 · 2 (x-2), y = 4x-6. Точка перетину дотичній і осі Ox: x1 =
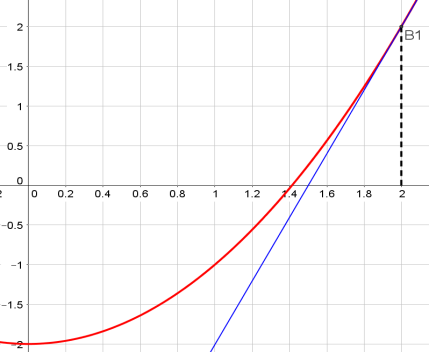
Мал. 3. Побудова першої дотичної до графіка функції f (x)
Потім знаходимо точку перетину функції y = f (x) і перпендикуляра, проведеного до осі Ox через точку x1. отримуємо точку В2 = (1.5; 0.25). Знову проводимо дотичну до функції y = f (x) в точці В2. і позначаємо точку перетину дотичної і Ox точкою x2.
Рівняння другої дотичній: y-2.25 = 2 * 1.5 (x-1.5), y = 3x - 4.25. Точка перетину дотичній і осі Ox: x2 =.
Потім знаходимо точку перетину функції y = f (x) і перпендикуляра, проведеного до осі Ox через точку x2. отримуємо точку В3 і так далі.
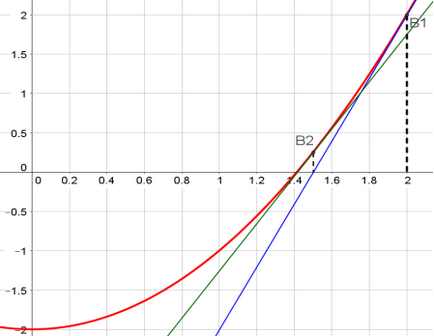
Мал. 4. Побудова другий дотичної до графіка функції f (x)
Перше наближення кореня визначається за формулою:
Друге наближення кореня визначається за формулою:
=
Третє наближення кореня визначається за формулою:
Таким чином, i -е наближення кореня визначається за формулою:
Обчислення ведуться до тих пір, поки не буде досягнуто збіг десяткових знаків, які необхідні у відповіді, або заданої точності e - до виконання нерівності | xi-xi-1 |