Критерій спільності системи лінійних рівнянь
Критерій спільності системи лінійних рівнянь дає теорема Кронекера-Капеллі.
Леопольд Кронекера (1823 - 1891 рр.) # 9472; німецький математик. Теорема, про яку піде мова, містилася в його лекціях, Новомосковсквшіх в Берлінському університеті в 1883 - 1891 рр.
Альфред крапель (1858 - 1916) # 9472; італійський математик. Він, мабуть, вперше дав формулювання теореми з використанням терміна «ранг матриці» в своїй роботі в 1892р.
Для того, щоб система лінійних рівнянь була сумісна, необхідно і достатньо, щоб ранг матриці системи дорівнював рангу розширеної матриці.
Приклад. Дослідити систему на спільність
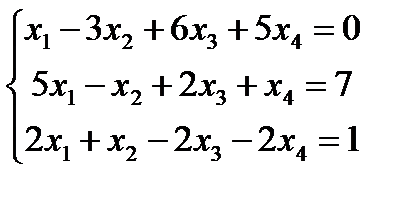
Рішення. Приведення матриці системи і розширеної матриці системи до східчастого увазі будемо виконувати одночасно.
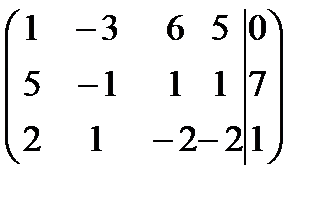
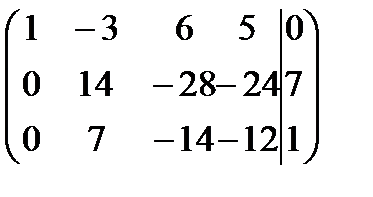
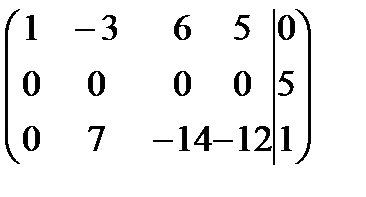
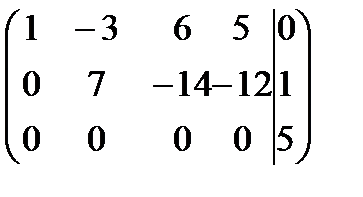
Ранг матриці системи дорівнює 2, а ранг розширеної матриці системи дорівнює 3. За теоремою Кронекера-Капеллі система несумісна.
Метод Гаусса рішення системи лінійних рівнянь.
Метод Гаусса застосовується для довільної системи лінійних рівнянь. Нам знадобиться
Визначення. Систему лінійних рівнянь будемо називати ступінчастою. якщо матриця цієї системи ступінчаста.
При вирішенні системи лінійних рівнянь застосуємо наступний алгоритм:
1. Записуємо розширену матрицю системи (1) і приводимо її до східчастого увазі,
визначаємо ранги матриці і розширеної матриці системи.
2. Якщо знайдені ранги не рівні, то система несумісна.
3. Ранг матриці системи дорівнює рангу розширеної матриці системи і дорівнює числу r. В
цьому випадку система сумісна і треба знайти її рішення.
4. Використовуючи ступінчастий вигляд розширеної матриці системи, записуємо відповідну ступінчасту систему.
5. Якщо число r дорівнює числу невідомих n, то ступінчаста система має вигляд
Із системи (2) послідовно знаходимо значення для х1. х2, ..., хт. починаючи з останнього рівняння. В цьому випадку система (1) має єдине рішення.
6. Якщо число r менше числа невідомих, то ступінчаста система має вигляд
В системі (3) r рівнянь і n невідомих. Невідомі х1, ..., хj1, які першими зустрічаються в рівняннях системи (3), назвемо головними невідомими. інші # 9472; вільними невідомими. Із системи (3) послідовно висловлюємо головні невідомі через вільні, починаючи з останнього рівняння. Вільні невідомі можуть приймати будь-які значення. В цьому випадку система має нескінченно багато рішень.
2)
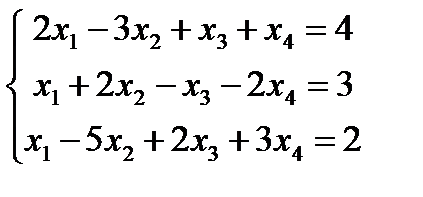
3)
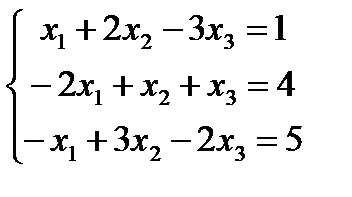
Правило Крамера рішення систем лінійних рівнянь.
Габріель Крамер (1704 - 1752) # 9472; швейцарський математик, який в 1750 р знайшов метод вирішення систем лінійних рівнянь, названий згодом правилом Крамера.
Визначення. Система лінійних рівнянь називається крамеровской, якщо тіло рівнянь дорівнює числу невідомих і визначник матриці системи відмінний від нуля.
Теорема 7.1. Крамеровская система має єдине рішення, яке знаходиться за формулами
де # 9472; визначник матриці системи, # 9472; визначник, отриманий з. заміною стовпця коефіцієнтів при на стовпець вільних членів.
Доведення. Нехай дана крамеровская система
# 9474; А # 9474; = # 8710; =
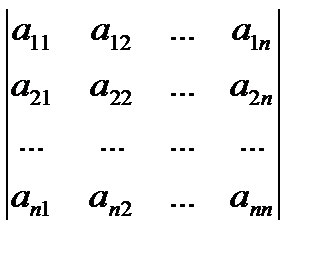
По теоремі 3 лекції 6 матриця системи А має зворотну матрицю А -1.
Запишемо крамеровскую систему (4) в матричному вигляді
Помножимо обидві частини матричного рівняння (5) зліва на А -1:
З огляду на асоціативності множення матриць маємо
А -1 (АХ) = (А -1 А) Х = ЕТ Х = Х.
Х = А -1 В # 9472; рішення системи.
1) Покажемо, що таке рішення єдино. Припустимо, що Х1 і Х2 # 9472; два рішення матричного рівняння (5). Тоді АХ1 = В і ах2 = В, звідки АХ1 = ах2. Помноживши обидві чисти рівності на А -1 зліва, маємо
Отже, система (4) має єдине рішення.
2) Знайдемо рішення системи (4). З рівності Х = А -1 В маємо:
=
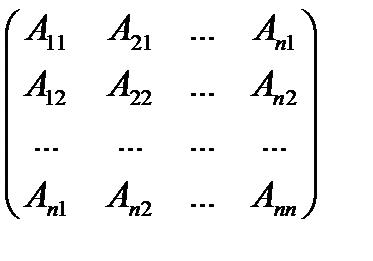
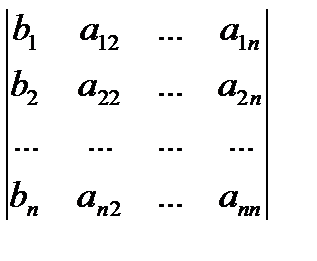
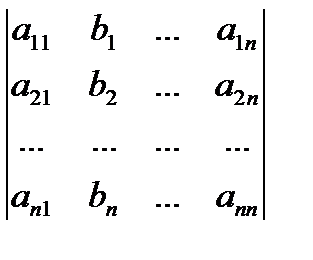
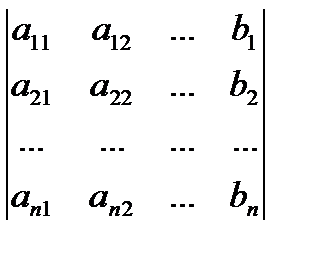
Позначаючи визначники в правій частині рівності відповідно, отримаємо формули.
Приклад. Вирішити систему рівнянь за правилом Крамера