9) Рішення невизначених систем лінійних рівнянь
Система m лінійних алгебраїчних рівнянь з n невідомими (чи, лінійна система, також вживається абревіатура СЛАР) в лінійної алгебри - це система рівнянь виду
Спільна слу - слу, що має одне або кілька рішень.
Невизначена слу - спільна слу, що має більше одного рішення.
Вирішується методом Жордана - Гаусса. Рішення виражаються по засобом вільних членів.
10) Однорідні системи лінійних рівнянь
СЛАР називається однорідною, якщо всі її вільні члени дорівнюють 0.
Теорема 1 (про нетривіальних рішень однорідної системи)
Однорідна лінійна система з квадратною матрицею має нетривіальне рішення тоді і тільки тоді, коли визначник системи дорівнює нулю.
Доказ По теоремі Крамера тоді і тільки тоді, коли система з квадратною матрицею має єдине рішення (тобто вектори - стовпці системи - лінійно залежні). У разі якщо задана система лінійних однорідних рівнянь, це рішення - тривіальне (0,0, ... 0). Значить, нетривіальні рішення є тоді і тільки тоді, коли (тобто. Рішень системи безліч).
Будь-яке рішення слоу виражається у вигляді лінійної комбінації
, ... ,.
Покажемо, що вектора - лінійно незалежні. Для цього складемо матріцуіз їх координат:
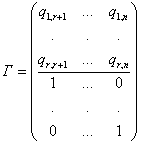
За межею розташований мінор порядку, відмінний від нулястолбцов матріцилінейно незалежні.
Отже, вектора - лінійно незалежні, тобто ці вектора утворюють базис підпростору.
Умова нетривіальною спільності:
Для того, щоб однорідна система мала нетривіальне рішення, необхідно і достатньо, щоб ранг її основної матриці був менше числа невідомих
Теорема Кронекера - Капеллі - критерій спільності системи лінійних алгебраїчних рівнянь:
Система лінійних алгебраїчних рівнянь сумісна тоді і тільки тоді, коли ранг її основної матриці дорівнює рангу її розширеної матриці, причому система має єдине рішення, якщо ранг дорівнює числу невідомих, і безліч рішень, якщо ранг менше числа невідомих.
11. Вектори. Лінійні операції над векторами
Геометричним вектором (або просто вектором) називається спрямований відрізок.
Вектор називається нульовим, якщо початок і кінець його співпадають. нульовий
вектор не має певного напряму і має довжину, рівну нулю. це
дозволяє при записі ототожнювати нульовий вектор з дійсним числом
Вектори називаються колінеарними, якщо вони лежать або на од-
ної прямої, або на паралельних прямих.
Два вектора називаються рівними, якщо вони колінеарні, мають оди-
наково довжину і однаковий напрямок.
Лінійні операції над векторами.
Лінійними операціями прийнято називати операцію додавання векторів і опе-
рацію множення векторів на речові числа.
Сумою a + b двох векторів a і b називається вектор, що йде
з початку вектора a в кінець вектора b за умови, що вектор b
прикладений до кінця вектора a.
1. a + b = b + a (переместительное властивість);
2. (a + b) + c = a + (b + c) (сочетательное властивість);
Різницею a - b вектора a і вектора b називається такий вектор
c, який в сумі з вектором b дає вектор a.
Твором α a (або aα) вектора a на дійсне число α
називається вектор b, колінеарний вектору a, що має довжину,
рівну | α | · | a |. і має напрямок, що збігається з направле-
ням вектора a в разі α> 0 і протилежний напрямку
вектора a в разі α <0.