Знайти проміжки зростання та спадання похідної функції в ЄДІ
\ (\ Blacktriangleright \) Якщо похідна позитивна на проміжку \ ((a; b) \). то функція на ньому строго зростає. \ (F '(x)> 0 \ Longrightarrow f (x) \ uparrow \)
Якщо похідна негативна на проміжку \ ((a; b) \). то функція на ньому строго убуває. \ (F '(x)<0 \Longrightarrow f(x) \downarrow\)
Зауважимо, що зворотні твердження невірні. Тобто якщо функція строго зростає на якомусь проміжку, то з цього не випливає, що на цьому проміжку її похідна буде позитивною. наприклад:
функція \ (f (x) = x ^ 3 \) на відрізку \ ([- 1; 1] \) строго зростає, але її похідна немає позитивна всюди: в точці \ (x = 0 \) її похідна \ (f ' (0) = 0 \) (тому що \ (f '(x) = 3x ^ 2 \)).
\ (\ Blacktriangleright \) Якщо функція не убуває (зростає і / або константа) на проміжку \ ((a; b) \). то на цьому проміжку її похідна неотрицательна (\ (\ geq 0 \)). Вірно і зворотне твердження.
\ (\ Blacktriangleright \) Якщо функція не збільшується (зменшується і / або константа) на проміжку \ ((a; b) \). то на цьому проміжку її похідна непозитивним (\ (\ leq 0 \)). Вірно і зворотне твердження.
\ (\ Blacktriangleright \) У точках зламу (на малюнку це точки \ (A \) і \ (B \)) похідною не існує.
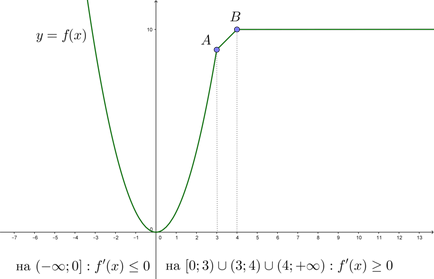
Зауважимо, що на проміжку \ ((4; + \ infty) \) похідна \ (f '(x) = 0 \). тому на цьому проміжку функція є константою (\ (f (x) = 10 \)).
Приклад: знайдіть кількість точок, в яких похідна дорівнює нулю, якщо на малюнку дано графік функції:

Похідна дорівнює нулю в точках \ (A, B, D \). а в точці \ (C \) вона не існує, тому що це точка зламу.
Випускна робота в формі ЄДІ для 11-класників обов'язково містить завдання на обчислення меж, проміжків убування і зростання похідної функції, пошук точок екстремуму і побудова графіків. Добре знання цієї теми дозволяє правильно відповісти на кілька запитань іспиту і не відчувати труднощів у подальшому професійному навчанні.
Основи диференціального обчислення - одна з головних тем математики сучасної школи. Вона вивчає застосування похідної для дослідження залежностей змінних - саме через похідну можна проаналізувати зростання і спадання функції без звернення до креслення.
Комплексна підготовка випускників до здачі ЄДІ на освітньому порталі «Школково» допоможе глибше зрозуміти принципи диференціювання - детально розібратися в теорії, вивчити приклади розв'язання типових задач і спробувати свої сили в самостійній роботі. Ми допоможемо вам ліквідувати прогалини в знаннях - уточнити уявлення про лексичних поняттях теми і залежностях величин. Учні зможуть повторити, як знаходити проміжки монотонності, що означає підйом або спадання похідної функції на певному відрізку, коли граничні точки включаються і не включаються до знайдені інтервали.
Вибираючи розділ «Конструктор», учні зможуть попрактикуватися в дослідженні зростання і зменшення похідної функції на реальних варіантах ЄДІ, постійно оновлюваних з урахуванням останніх змін і нововведень.