Визначення момет інерції махового колеса
Приналежності: установка; набір вантажів; лінійка; штангенциркуль; секундомір; ваги.
У даній роботі момент інерції колеса визначається двома методами.
На шків А (або В) намотується нитка з прикріпленим до неї вантажем Р (рис. 1). Падаючи вантаж розмотує нитку і призводить систему (махове колесо К, шківи А і В, вісь С) в обертальний рух. При цьому потенційна енергія вантажу переходить в кінетичну енергію вантажу і кінетичну енергію обертального руху системи.
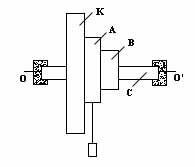
На підставу закону збереження енергії можна записати:
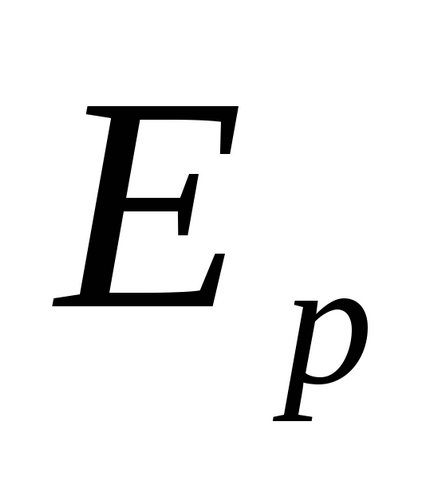
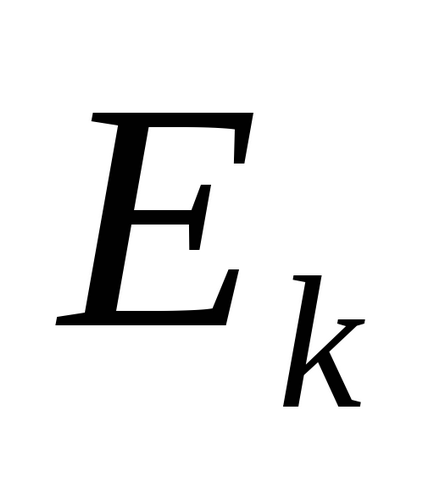
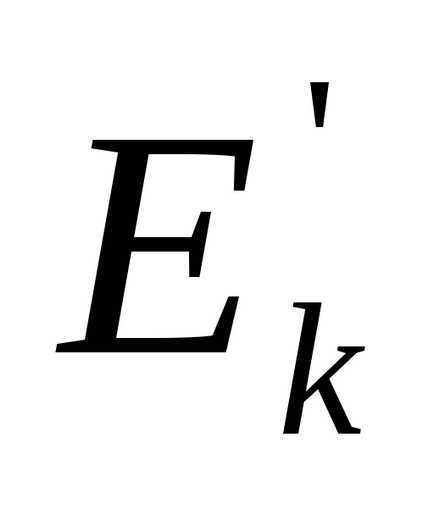
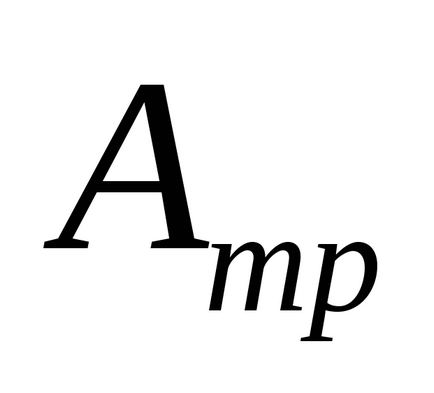
Введемо позначення: m - маса вантажу; h - максимальна висота його підйому; V - швидкість вантажу в нижньому положенні; r- радіус шківа; Io - момент інерції системи; - її кутова швидкість в момент, коли вантаж досягає нижнього положення.
Тоді рівняння (I) може бути переписано у вигляді:
Так як момент сил тертя не залежить від швидкості обертання, то рух системи буде рівноприскореному.
Знаючи висоту h і час руху грузаt. легко підрахувати його швидкість в нижньому положення:
Якщо нитка розмотується без ковзання, то лінійна швидкість точок на поверхні шківа дорівнює швидкості вантажу і
Робота проти сил тертя пропорційна числу оборотів, що здійснюються системою, тобто
де
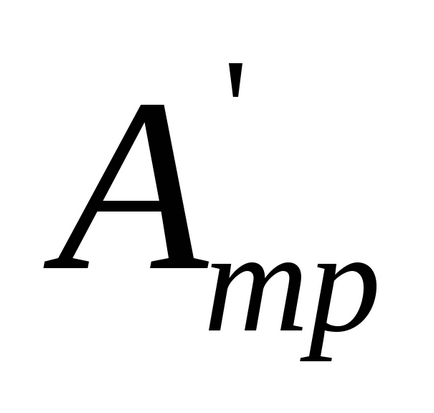
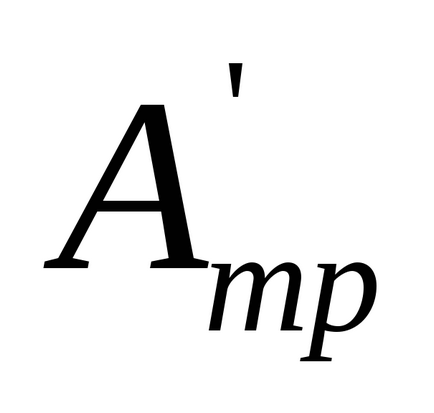
У момент досягнення вантажем нижнього положення нитка відділяється від шківа, а система продовжує обертатися, здійснюючи роботу проти сил тертя за рахунок придбаної кінетичної енергії
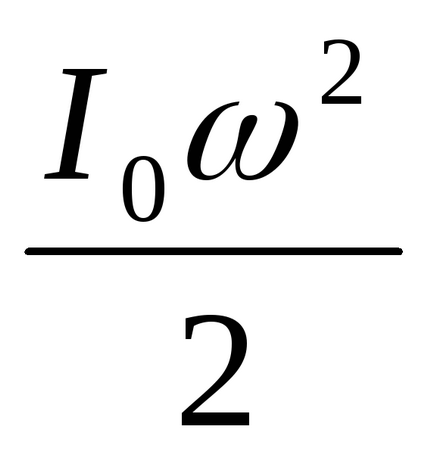
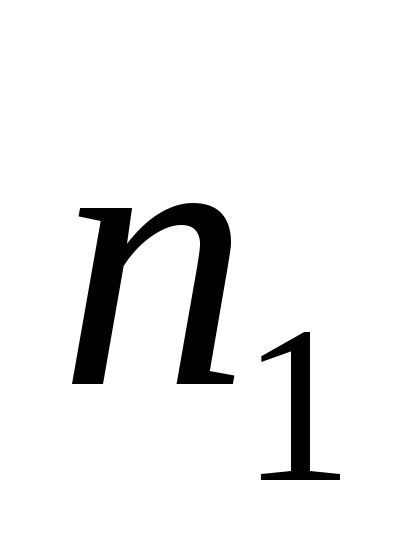
Використовуючи співвідношення (3), (4), (5), (6) і (7), можна уявити (2) в наступному вигляді:
,
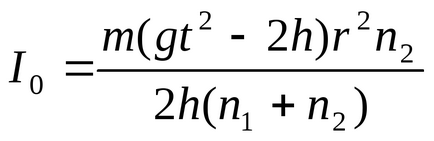
Всі величини, що входять в праву частину цієї рівності можуть бути виміряні на досвіді.
Якщо на деякому расcтоянііl від центру колеса прикріпити до нього додатковий грузQ (рис. 2), то система перетворюється в фізичний маятник.
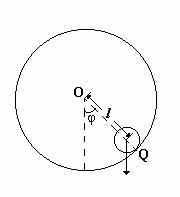
Виведений з положення рівноваги, маятник буде коливатися під дією моменту сили тяжіння додаткового вантажу. Нехтуючи силами тертя, можна записати рівняння руху маятника у вигляді:
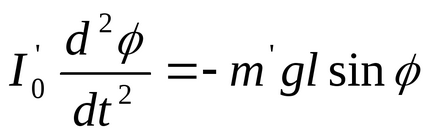
де
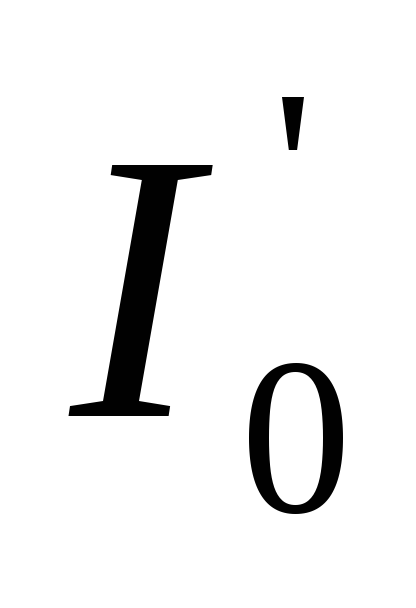
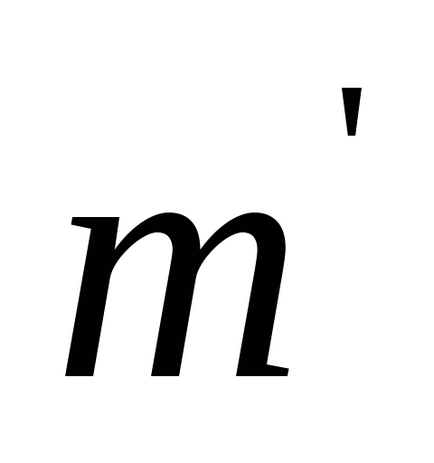
Для малих кутів
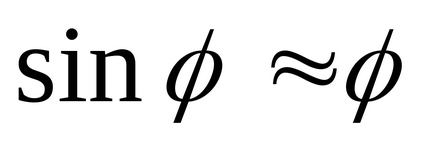
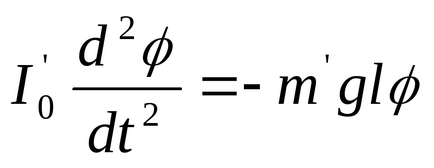
Рівняння (8) являє собою рівняння гармонійних коливань з періодом
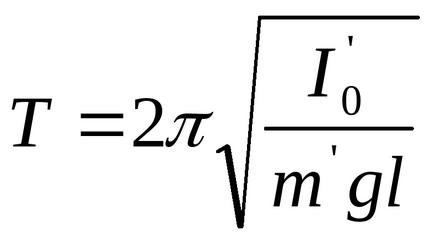
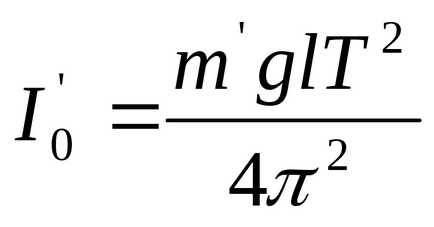
1. Визначення моменту інерції системи методом обертання.
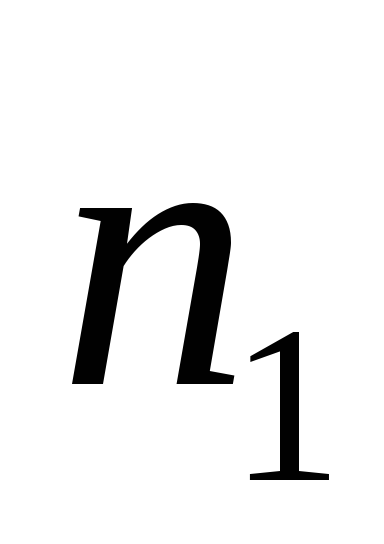
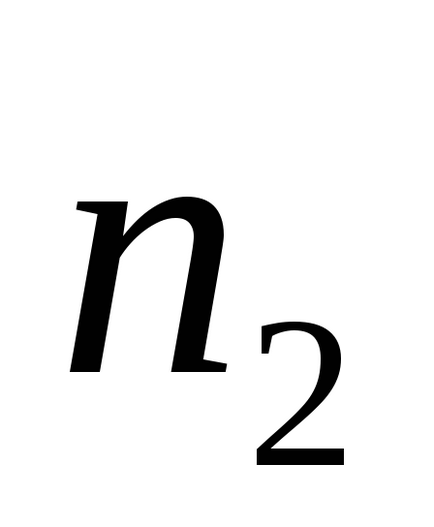
Експеримент проводився для 2-х різних вантажів і на 2-х різних шківах різного радіусу.
А) m = 249г; d = 7.47 см; r = 3.75см; h = 163см.