Вектори і скаляри - студопедія
Величини, для завдання яких досить одного числового значення, називаються скалярними. Прикладами скалярів можуть служити шлях, маса, час і т. Д.
Величини, для завдання яких необхідні числове значення і напрямок, називають векторами. Прикладами векторів є, наприклад, переміщення, швидкість, прискорення, сила і т. Д. Вектори прийнято позначати буквами зі стрілкою (,.,). При відсутності стрілки та ж буква означає числове значення або модульсоответствующего вектора. Таким чином, модуль вектора.
Модуль вектора - скаляр, причому завжди позитивний. Показана на рис. П. 1а операція додавання векторів символічно записується в такий спосіб:
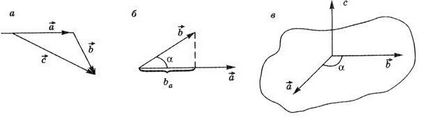
В результаті множення вектора на скаляр а виходить новий вектор, модулькоторого в а разів більше вектора, а напрямок збігається з напрямком вектора, якщо скаляр позитивний, і протилежно йому, якщо скаляр негативний.
Скалярний добуток двох векторів і - це скалярна величина, що дорівнює добутку модулів векторів і, помноженому на косинус кута між ними:
де в формулу введена проекція вектора на напрямок вектора (BА = b cos # 945;) (рис. П.1б).
Векторний добуток векторів і - це вектор, який дорівнює за модулем добутку модулів векторів і на синус кута # 945; між ними (рис. П.1в).
Вектор перпендикулярний площині, в якій лежать вектори і, його напрямок можна знайти, наприклад, за правилом правого гвинта - обертальний рух гвинта повинен співпадати з напрямом найкоротшого повороту від до, тоді його поступальний рух дає напрямок.
2. Градієнт скалярної велічіниa. Нехай в просторі будь-яким чином розподілена скалярна величина а - це може бути поле температури (а = Т), потенційної енергії (а = U) і т. Д. Таке поле можна охарактеризувати градієнтом а. Під градієнтом скалярної величини розуміють вектор, який в кожній точці простору спрямований в бік найбільш швидкого зростання а й чисельно рівний збільшенню величини а на одиницю довжини цього напрямку.
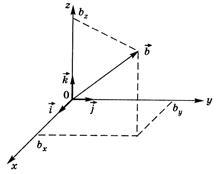
При обчисленні похідної величини а по координаті х у формулі (п.4) вважається, що координати y і z залишаються постійними - така похідна називається приватної похідною по координаті х:
Аналогічні припущення приймаються при розрахунку приватних похідних по координатам y і z.
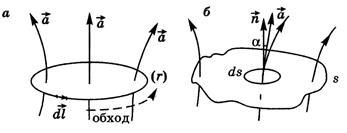
Візьмемо в неоднорідному полі уявний замкнутий контур Г. вкажемо довільно напрямок його обходу і введемо вектор, рівний по модулю елементарної довжині dlконтура. У кожній точці вектор збігається з дотичною до контуру і спрямований по обходу контуру (рис. П.3а).
Тоді циркуляцією вектора по довільному замкненому контуру Г називають інтеграл такого вигляду:
Можна стверджувати, що якщо для поля вектора циркуляція вектора по довільному замкненому контуру Г дорівнює нулю, то це поле є потенційним (наприклад, електростатичне поле вектора). Якщо ж циркуляція за довільним замкнутому контуру Г відмінна від нуля, то поле вектора не є потенційним, його називають вихровим полем.
Введемо поняття потоку Ф вектора. Візьмемо в неоднорідному полі вектора довільну поверхню S. виділимо на ній елементарну площадку dS і введемо вектор, спрямований уздовж вектора нормалі до площадки (рис. П.3б). Модуль дорівнює площі dS елементарної площадки.
Тоді елементарним потоком dФ вектора черезплощадку dS називають величину
Підсумовуючи потоки dФ через всі майданчики dS поверхні S. знайдемо потік вектора через поверхню S:
Якщо врахувати, що густота вектора визначає модуль вектора в даній точці поля, то тоді потік вектора чисельно дорівнює кількості N ліній, які пронизують поверхню S.
4. Дивергенція і ротор вектора .Для вирішення практичних завдань необхідно застосовувати математичний апарат, що дозволяє враховувати тип векторних полів не тільки у великому обсязі простору, але і в малій околиці будь-якої точки. Для цього вводяться поняття дивергенції () і ротора () вектора.
Візьмемо обсяг поля V. обмеженого замкнутою поверхнею S. і будемо стягіватьповерхность в малу околиця точки А (рис. П.4а)
Тоді дивергенцией вектора називають межа
Дивергенція характеризує наявність джерел першого типу в малій околиці точки А, наприклад, електричних зарядів (рис. П.5а):
де # 961; - щільність заряду.
В математиці для можна записати наступний вираз: