теорія ігор
Теорія ігор. Рішення матричної гри, приклад.
Гра задана платіжною матрицею. Визначити оптимальні стратегії гравців, стратегію першого визначити геометрично, а стратегію другого - за допомогою симплекс-методу.
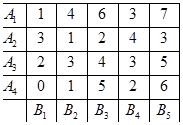
Рішення:
З'ясуємо, чи є тут сідлова точка.
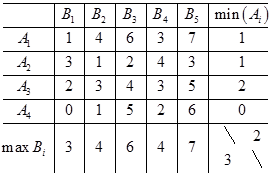
Нижня ціна гри
Верхня ціна гри
Оскільки нижня ціна не дорівнює верхній ціною, то сідлової точки немає, тобто рішення матричної гри потрібно шукати в змішаних стратегіях.
Досліджуємо матрицю з точки зору домінування.
Стратегія домінує над стратегією, тому що всі елементи п'ятого стовпчика більше відповідних елементів другого стовпця. Приберемо п'ятий стовпець.
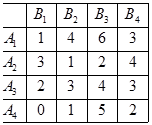
Стратегія домінує над стратегією.
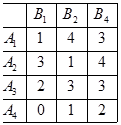
Стратегія домінує над стратегією.
Стратегія строго доминируется стратегією.
Отримали матрицю виграшів, де у гравців А і В немає домінуючих стратегій.
Спочатку знайдемо оптимальну стратегію гравця В. Зауважимо, що і вирішимо наступну задачу лінійного програмування:
Мінімізувати функцію при обмеженнях:
Оскільки змінних всього дві, то це завдання лінійного програмування найпростіше вирішити графічним способом. Побудуємо безліч допустимих рішень, тобто область, яка описується цими нерівностями і обмежену прямими:
По осі абсцис будемо відкладати. а по осі ординат. Область допустимих значень зафарбована жовтим кольором.
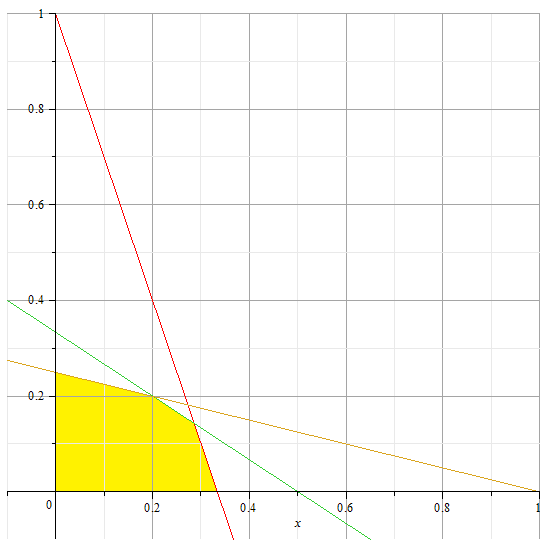
Будуємо лінії рівня. які мають вигляд. де С - довільна стала. Розуміємо, що для збільшення С пряма повинна займати максимально «високе» положення, але маючи з областю допустимих рішень хоча б одну точку.
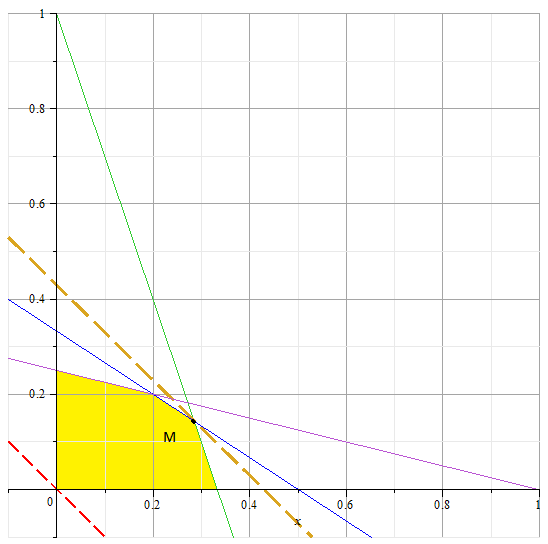
Такий стан прямий - проходить через точку М. Знайдемо її координати як перетин двох прямих.
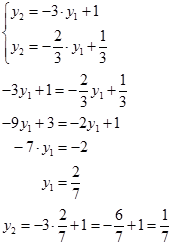
Отримали. тоді
і