Приклади матричних ігор у чистій і змішаної стратегії зменшення порядку платіжної матриці -
2.2 Приклади матричних ігор у чистій і змішаної стратегії Зменшення порядку платіжної матриці
Порядок платіжної матриці (кількість рядків і стовпців) може бути зменшений за рахунок виключення домінованих і дублюючих стратегій.
Стратегія K * називається домінованих стратегією K **, якщо при будь-якому варіанті поведінки протидіє гравця виконується співвідношення
де і - значення виграшів при виборі гравцем, відповідно, стратегій K * і K **.
У разі, якщо виконується співвідношення
=,
стратегія K * називається дублюючої по відношенню до стратегії K **.
Наприклад, в матриці
Платіжна матриця з домінованих і дублюючими стратегіями. Стратегія A1 є домінованих по відношенню до стратегії A2, стратегія B6 є домінованих по відношенню до стратегій B3, B4 і B5, а стратегія B5 є дублюючої по відношенню до стратегії B4. Дані стратегії не будуть обрані гравцями, так як є свідомо програшними і видалення цих стратегій з платіжної матриці не вплине на визначення нижньої і верхньої ціни гри, описаної даної матрицею.
Безліч недомініруемих стратегій, отриманих після зменшення розмірності платіжної матриці, називається ще безліччю Парето (по імені італійського економіста Вільфредо Парето, який займався дослідженнями в даній області)
Приклад рішення матричної гри в чистих стратегіях
Розглянемо приклад вирішення матричної гри в чистих стратегіях, в умовах реальної економіки, в ситуації боротьби двох підприємств за ринок продукції регіону.
Два підприємства виробляють продукцію і поставляють її на ринок регіону. Вони є єдиними постачальниками продукції в регіон, тому повністю визначають ринок даної продукції в регіоні.
Кожне з підприємств має можливість виробляти продукцію із застосуванням однієї з трьох різних технологій. Залежно від якості продукції, виробленої з кожної технології, підприємства можуть встановити ціну одиниці продукції на рівні 10, 6 і 2 грошових одиниць відповідно. При цьому підприємства мають різні витрати на виробництво одиниці продукції.
Витрати на одиницю продукції, виробленої на підприємствах регіону (ВО).
Ціна реалізації одиниці продукції, грн
Повна собівартість одиниці продукції, грн
Значення часткою продукції підприємства 1, придбаної населенням, залежать від співвідношення цін на продукцію підприємства 1 і підприємства 2. В результаті маркетингового дослідження ця залежність встановлена і значення обчислені.
Частка продукції підприємства 1, що купується населенням в залежності від співвідношення цін на продукцію (табл. 1.1)
Ціна реалізації 1 од. продукції, Д.Є.
Частка продукції підприємства 1, купленої населенням
За умовою завдання на ринку регіону діє тільки 2 підприємства. Тому частку продукції другого підприємства, придбаної населенням, в залежності від співвідношення цін на продукцію можна визначити як одиниця мінус частка першого підприємства.
Стратегіями підприємств в даній задачі є їх рішення щодо технологій виробництва продукції. Ці рішення визначають собівартість і ціну реалізації одиниці продукції. У задачі необхідно визначити:
1. Чи існує в даній задачі ситуація рівноваги при виборі технологій виробництва продукції обома підприємствами?
2. Чи існують технології, які підприємства свідомо не будуть вибирати внаслідок невигідності?
3. Скільки продукції буде реалізовано в ситуації рівноваги? Яке підприємство опиниться у виграшному становищі?
1. Визначимо економічний сенс коефіцієнтів виграшів в платіжній матриці завдання. Кожне підприємство прагне до максимізації прибутку від виробництва продукції. Але крім того, в даному випадку підприємства ведуть боротьбу за ринок продукції в регіоні. При цьому виграш одного підприємства означає програш іншого. Таке завдання може бути зведена до матричної грі з нульовою сумою. При цьому коефіцієнтами виграшів будуть значення різниці прибутку підприємства 1 і підприємства 2 від виробництва продукції. У разі, якщо ця різниця позитивна, виграє підприємство 1, а в разі, якщо вона негативна - предпріятіе2.
2. Розрахуємо коефіцієнти виграшів платіжної матриці. Для цього необхідно визначити значення прибутку підприємства 1 і підприємства 2 від виробництва продукції. Прибуток підприємства в даній задачі залежить:
- від ціни і собівартості продукції;
- від кількості продукції, що купується населенням регіону;
- від частки продукції, придбаної населенням у підприємства.
Таким чином, значення різниці прибутку підприємств, що відповідають коефіцієнтам платіжної матриці, необхідно визначити за формулою (1):
D = p × (S × R1-S × C1) - (1-p) × (S × R2-S × C2) (1),
де D - значення різниці прибутку від виробництва продукції підприємства 1 і підприємства 2;
p - частка продукції підприємства 1, що купується населенням регіону;
S - кількість продукції, що купується населенням регіону;
R1 і R2 - ціни реалізації одиниці продукції підприємствами 1 і 2;
C1 і C2 - повна собівартість одиниці продукції, виробленої на підприємствах 1 і 2.
Обчислимо один з коефіцієнтів платіжної матриці.
Нехай, наприклад, підприємство 1 приймає рішення про виробництво продукції відповідно до технології III, а підприємство 2 - відповідно до технології II. Тоді ціна реалізації одиниці. продукції для підприємства 1 складе 2 ВО при собівартості одиниці. продукції 1,5 Д.Є. Для підприємства 2 ціна реалізації одиниці. продукції складе 6 Д.Є. при собівартості 4 Д.Є. (Табл. 1.1).
Кількість продукції, яку населення регіону придбає при середній ціні 4 Д.Є. дорівнює 4 тис. од. (Таблиця 1.2). Частка продукції, яку населення придбає у підприємства 1, складе 0,85, а у підприємства 2 - 0,15 (табл. 1.3). Обчислимо коефіцієнт платіжної матриці a32 за формулою (1): a32 = 0,85 × (4 × 2-4 × 1,5) - 0,15 × (4 × 6-4 × 4) = 0,5 тис. Од.
де i = 3 - номер технології першого підприємства, а j = 2 - номер технології другого підприємства.
Аналогічно обчислимо всі коефіцієнти платіжної матриці. У платіжної матриці стратегії A1 - A3 - представляють собою рішення про технології виробництва продукції підприємством 1, стратегії B1 - B3 - рішення про технології виробництва продукції підприємством 2, коефіцієнти виграшів - різницю прибутку підприємства 1 і підприємства 2. Платіжна матриця в грі «Боротьба двох підприємств за ринок продукції регіону ».
У даній матриці немає ні домінованих, ні дублюючих стратегій. Це означає, що для обох підприємств немає свідомо невигідних технологій виробництва продукції. Визначимо мінімальні елементи рядків матриці. Для підприємства 1 кожен з цих елементів має значення мінімально гарантованого виграшу при виборі відповідної стратегії. Мінімальні елементи матриці по рядках мають значення: 0,17, -1,5, 0,4.
Визначимо максимальні елементи стовпців матриці. Для підприємства 2 кожен з цих елементів також має значення мінімально гарантованого виграшу при виборі відповідної стратегії. Максимальні елементи матриці по стовпцях мають значення: 3, 0,62, 0,4.
Нижня ціна гри в матриці дорівнює 0,4. Верхня ціна гри також дорівнює 0,4. Таким чином, нижня і верхня ціна гри в матриці збігаються. Це означає, що є технологія виробництва продукції, яка є оптимальною для обох підприємств в умовах даного завдання. Ця технологія III, яка відповідає стратегіям A3 підприємства 1 і B3 підприємства 2. Стратегії A3 і B3 - чисті оптимальні стратегії в даній задачі.
Значення різниці прибутку підприємства 1 і підприємства 2 при виборі чистої оптимальної стратегії позитивно. Це означає, що підприємство 1 виграє в даній грі. Виграш підприємства 1 складе 0,4 тис. Д.Є. При цьому на ринку буде реалізовано 5 тис. Од. продукції (реалізація дорівнює попиту на продукцію, таблиця 1.2). Обидва підприємства встановлять ціну за одиницю продукції в 2 ВО При цьому для першого підприємства повна собівартість одиниці продукції складе 1,5 Д.Є. а для другого - 1 д.е (таблиця 1.1). Підприємство 1 виявиться у виграші лише за рахунок високої частки продукції, яку придбає у нього населення.
Змішані стратегії в матричних іграх
Поняття про матричних іграх зі змішаним розширенням
Дослідження в матричних іграх починається з знаходження її чистою ціни. Якщо матрична гра має рішення в чистих стратегіях, то знаходженням чистої ціни закінчується дослідження гри. Якщо ж в грі немає рішення в чистих стратегіях, то можна знайти нижню і верхню ціни цієї гри, які вказують, що гравець 1 не повинен сподіватися на виграш більший, ніж верхня ціна гри, і може бути впевнений в отриманні виграшу не менше нижньої ціни гри . Поліпшення рішень матричних ігор слід шукати у використанні секретності застосування чистих стратегій і можливості багаторазового повторення ігор у вигляді партії. Цей результат досягається шляхом застосування чистих стратегій випадково, з певною ймовірністю.
Визначення. Змішаною стратегією гравця називається повний набір чистих стратегій, застосованих відповідно до встановленого розподілу ймовірностей. Матрична гра, яке вирішується за використанням змішаних стратегій, називається грою зі змішаним розширенням.
Стратегії, застосовані з ймовірністю, відмінною від нуля, називаються активними стратегіями.
Доведено, що для всіх ігор із змішаним розширенням існує оптимальна змішана стратегія, значення виграшу при виборі якої знаходиться в інтервалі між нижньою і верхньою ціною гри:
Vн £ V £ V ст.
При цьому умови величина V називається ціною гри.
Крім того, доведено, що, якщо один з гравців дотримується своєї оптимальної змішаної стратегії, то виграш залишається незмінним і рівним ціні гри V, незалежно від того, яких стратегій дотримується інший гравець, якщо тільки він не виходить за межі своїх активних стратегій. Тому, для досягнення найбільшого гарантованого виграшу другому гравцеві також необхідно дотримуватися своєї оптимальної змішаної стратегії.
Рішення матричних ігор із змішаним розширенням методами лінійного програмування
Рішення матричної гри зі змішаним розширенням - це визначення оптимальних змішаних стратегій, тобто знаходження таких значень ймовірностей вибору чистих стратегій для обох гравців, при яких вони досягають найбільшого виграшу.
Для матричної гри, платіжна матриця якої показана на рис. 1.1, Vн ¹ Vв. визначимо такі значення ймовірностей вибору стратегій для гравця 1 (p1. p2, ..., pm) і для гравця 2 (q1. q2, ..., qn), при яких гравці досягали б свого максимально гарантованого виграшу.
Якщо один з гравців дотримується своєї оптимальної стратегії, то, за умовою задачі, його виграш не може бути меншою за ціну гри V. Тому дана задача може бути представлена для гравців у вигляді наступних систем лінійних нерівностей:
Для першого гравця:
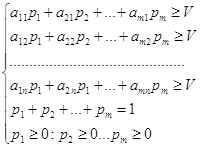
Для другого гравця:
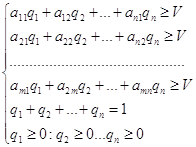
Щоб визначити значення V, розділимо обидві частини кожного з рівнянь на V. Величину pi / V позначимо через xi. а qj / V - через yj.
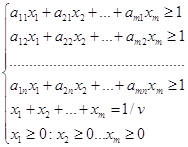
Для гравця 1 отримаємо наступну систему нерівностей, з якої знайдемо значення 1 / v:
Для гравця 1 необхідно знайти максимальну ціну гри (V). Отже, значення 1 / V має прагнути до мінімуму.
Цільова функція задачі буде мати наступний вигляд:
Для гравця 2 отримаємо наступну систему нерівностей, з якої знайдемо значення 1 / v:
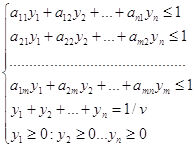
Для гравця 2 необхідно знайти мінімальну ціну гри (V). Отже, значення 1 / V має прагнути до максимуму.
Цільова функція задачі буде мати наступний вигляд:
Всі змінні в даних системах лінійних нерівностей повинні бути невід'ємними: xi = pi / V, а yi = qj / V. Значення pi і qj не можуть бути негативними, так як є значеннями ймовірностей вибору стратегій гравців. Тому необхідно, щоб значення ціни гри V не було негативним. Ціна гри обчислюється на основі коефіцієнтів виграшів платіжної матриці. Тому, для того, щоб гарантувати умова невід'ємності для всіх змінних, необхідно, щоб всі коефіцієнти матриці були невід'ємними. Цього можна домогтися, додавши перед початком виконання завдання до кожного коефіцієнту матриці число K, відповідне модулю найменшого негативного коефіцієнта матриці. Тоді в результаті виконання завдання буде визначена не ціна гри, а величина
Для вирішення завдань лінійного програмування використовується симплекс-метод. [1, 5].
В результаті рішення визначаються значення цільових функцій (для обох гравців ці значення збігаються), а також значення змінних xi і yj.
Величина V * визначається за формулою: V * = 1 / z
Значення ймовірностей вибору стратегій визначаються: для гравця 1: Pi = xi × V *: для гравця 2: qi = yi × V *.
Для визначення ціни гри V з величини V * необхідно відняти число K.
Приклад рішення матричної гри зі змішаним розширенням
Розглянемо приклад вирішення матричної гри зі змішаним розширенням. Платіжну матрицю гри складемо на основі вихідних даних, замінивши лише значення часткою продукції підприємства 1, що купується населенням в залежності від співвідношень цін (табл. 2.1).
Таблиця 2.1 - Частка продукції підприємства 1, що купується населенням в залежності від співвідношення цін на продукцію
Ціна реалізації 1 од. продукції, Д.Є.
Частка продукції підприємства 1, купленої населенням