Теорія 2x2 завдання на переливання
Всі завдання на переливання принципово діляться на 2 типу.
Перший - коли у нас є багато рідини (озеро, нескінченно велика бочка, водопровід), і ми можемо наповнювати доверху судини як завгодно велику кількість разів, тобто кількість рідини не обмежена. При цьому ми можемо безбоязно виливати воду з судин.
Також варто зрозуміти принцип завдань на переливання: наприклад, якщо у нас є посудину об'ємом 8 літрів і 5 літрів, і нам треба відміряти 2 літри води, ми не маємо права на наступне рішення: «Наповнимо восьмилітровий посудину на чверть - таким чином, ми і отримаємо 2 літри води ». Або: «Давайте спустошимо наш 5 літровий сосуд на 60%, тоді в ньому залишиться рівно 2 літри води». Ні, так робити не можна. (Якщо у дитини в цьому місці виникають питання, то ви можете придумати, наприклад, таке оригінальне пояснення: «А раптом наш посудину - це якась хитромудра ваза (або древня амфора), звичайно, без шкали поділок!» Або навіть просто банку не цілком симетрична, а на око визначити середину - проблематично ...) Ми можемо або повністю наповнювати судини, або повністю спустошувати їх, або переливати з однієї судини в іншій. При цьому ми можемо користуватися тим, що при цих операціях частина води може залишатися в посудині, з якого доповнюється іншу посудину.
Для прикладу вирішимо три завдання.
Завдання 1-го типу
Для приготування компоту мамі потрібно налити в 5-літрову каструлі 4 літри води. Як мамі впоратися з цим завданням, якщо у мами є крім цієї каструлі ще 3-літрова банка, водопровідний кран і раковина, куди можна виливати воду?
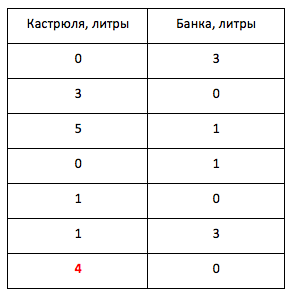
Наллємо в 3-літрову банку воду і Переллємося її в каструлю. Потім ще раз наповнимо банку і вильyoм в каструлю, скільки поміститься. Тоді в каструлі буде 5 літрів і 1 літр в 3-літровій банці. Тепер виллємо всю воду з каструлі в раковину. Потім переллємо літр з банки в каструлю і додамо ще три літри, наповнивши банку ще раз. Тепер в каструлі 1 + 3 = 4 літри, що і було потрібно. Завдання вирішена.
Наше рішення можна проілюструвати таблицею:
Завдання 2-го типу
У Марії є 2 глечика обсягом 8 і 3 літри. У восьмилітровим глечику налитий весь наявний у Марії кисіль. Як відміряти 2 літри киселю? Всі надлишки киселю можна віддати Коту Баюн, який просто обожнює ці ласощі.
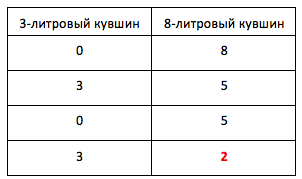
Наповнимо трилітровий глечик доверху з восьмилітровим, після цього у нас буде 5 літрів в 8-літровому і 3 літри в 3-літровому. Віддамо весь кисіль з 3-літрового глечика Коту Баюн. Після цього у нас залишилося 5 літрів в 8-літровому і 3-літровий глечик порожній. Знову наповнимо 3-літровий глечик з 8-літрового. Після цієї операції в 8-літровому глечику у нас залишиться рівно 2 літри (5 - 3 = 2). Ми відміряли 2 літри. Завдання вирішена!
Рішення також можна проілюструвати таблицею:
Ще одне завдання 2-го типу
У каструлі налито 8 літрів супу. Є також порожні 3-х і 5-тілітровая банки. Потрібно відміряти 4 літри супу. Як це зробити, якщо суп не можна проливати?
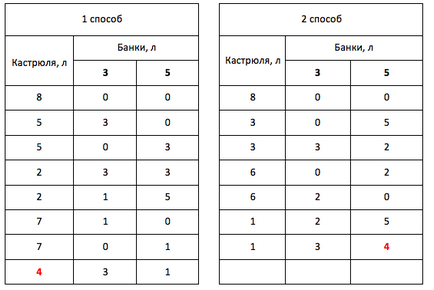
1 спосіб. Наллємо суп доверху в меншу банку, потім Переллємося отримані три літри в 5-літрову банку, а 3-літрову наповнимо знову. Тепер будемо лити суп з 3-літрової банки в 5-літрову, поки вона не наповниться доверху. Тоді в меншій банку залишиться 1 літр (5 - 3 = 2 і 3 - 2 = 1). Переллємося 5 літрів в каструлю, а 1 літр - у велику банку. Потім Переллємося 3 літри з каструлі в меншу банку. Після цього в каструлі залишиться рівно 4 літри. Завдання вирішена.
2 спосіб. Наллємо суп доверху в велику банку, тоді в каструлі залишиться рівно 3 літр. Переллємося з великою банки в меншу 3 літри, після чого Переллємося їх в каструлю. Переллємося 2 літри з великою банки в меншу, і наповнимо велику банку доверху супом з каструлі. Після чого дольyoм меншу банку (там було 2 літри, а поміщається 3) з більшою банки. Отримаємо 4 літри в великій банці. Завдання вирішена.
Проілюструємо обидва способи таблицями:
Також дитині можна дати наступну підказку. Йтиметься про завдання, де дозволяється виливати рідини. Нехай в якийсь момент наповнені всі судини, може бути, частково. Тоді перед дитиною стоїть питання про те, звідки вилити рідину. Виливати варто з повного судини, а не з напівпорожнього, так як кількість літрів в повному посудині ми завжди з легкістю знову отримаємо, тоді як отримати напівпорожній посудину - справа скрутне. Сподіваємося, що в процесі роботи ви самі зможете придумати безліч оригінальних прийомів і способів!
Зверніть увагу, що наведені рішення можуть не бути єдиними. Ні в якому разі не кажіть дитині, що він якось не так став вирішувати завдання, якщо першим ходом він, припустимо, налив воду з крана не в більший, а в менший посудину! Просто ретельно стежте за його діями. У більшості завдань є як мінімум 2 способи вирішення, і, швидше за все, при правильному виконанні переливань ваша дитина в кінцевому підсумку отримає результат. Правда, можливо, за більше число ходів, зате - скільки задоволення від самостійного рішення без підказок він отримає!
Випробуйте свої знання!
Для самих розумних і талановитих учнів ми проводимо на сайті дистанційну інтернет-олімпіаду. Відразу ж після проходження олімпіади показуються результати і повний розбір завдань для роботи над помилками. Залежно від успіхів олімпіадника видаються електронні дипломи та похвальні грамоти.
Кожен учасник отримує електронний сертифікат учасника.