Складна процентна ставка
Складна процентна ставка
Складна процентна ставка нарощення - це процентна ставка, при якій база нарахування, на відміну від простих відсотків, є п е р е м е н н о й. тобто відсотки нараховуються на відсотки.
Також заздалегідь обмовляється деякий одиничний проміжок нарахування відсотків (рік, місяць, квартал і т.д.) і ставка відсотка i (або i% = 100 i). Нехай початкова сума боргу дорівнює P. Тоді через одиничний проміжок сума боргу складе S 1 = P (1 + i), як і в випадку простих відсотків. Однак до кінця 2-го одиничного проміжку сума боргу складе S 2 = S 1 (1 + i) = P (1 + i) 2 (на відміну від формули S 2 = P (1 + 2 i) для простих відсотків. До кінця 3-го періоду отримуємо S 3 = S 2 (1 + i) = P (1 + i) 3. І так далі До кінця n-го одиничного проміжку одержуємо
Отже, через n проміжків початкова сума P збільшиться в (1+ i) n раз. Множник (1 + i) n називається множником нарощення. Відзначимо, що нарощення за складними відсотками являє зростання початкової суми за законом геометричної прогресії, перший член якої дорівнює P. а знаменник 1+ i.
Завдання 1. Початкова сума вкладу P = 40 000 р. Відсоткова ставка i% = 10% річних. Визначити наращѐнную по складним відсоткам за 3 роки, а потім порівняти її з сумою нарощення за схемою простих відсотків.
Рішення. Застосовуючи формулу (1) маємо
S 3, складність = P (1 + i) 3 = 40 000 (1 + 0.1) 3 = 53 240 р.
Обчислимо наращѐнную суму за схемою простих відсотків:
S 3, пр = P (1 + 3 i) = 40 000 (1 + 0.3) = 52 000 р. <53 240 р.
Отже, в даному випадку використання складних відсотків призводить до більшої наращѐнной сумі, що вигідніше вкладнику в порівнянні з нарощенням за схемою простих відсотків.
Формула нарощення складних відсотків (1), виведена для цілих
позитивних n. застосовна і для нецілих t
Тут P - початкова сума, n k - тривалість k -го періоду нарахування відсотків і i k - ставка простих відсотків в періоді з номером k.
Завдання 3. У договорі про обслуговування банківського вкладу протягом 4-х років зафіксована змінна ставка складних відсотків наступним чином. У 1-й рік - 6% річних, у 2-й і 3-й рік ставка одна і та ж - 5% річних, в 4-й рік
- 8%. Визначити величину множника нарощення за 4 роки.
Рішення. Нехай P - деяка початкова сума. За умовою завдання
i 1 = 0.06, i 2 = i 3 = 0.05, i 4 = 0.08.
Позначимо i 23 = 0.05. Маємо відповідно до формули (2):
S = P (1 i 1) 1 (1 i 23) 2 (1 i 4) 1 = P (1 + 0.06) (1 + 0.05) 2 (1 + 0.08).
В результаті обчислень отримуємо значення множника нарощення:
S / P = (1 + 0.06) (1 + 0.05) 2 (1 + 0.08) = 1.262142.
Порівняння сили росту простих і складних відсотків
При одній і тій же ставці відсотка i нарощення складних відсотків:
йде швидше, ніж простих відсотків, якщо довжина періоду нарощення більше одиничного періоду;
йде повільніше, ніж простих відсотків, якщо довжина періоду нарощення менше одиничного періоду.
Раніше було відзначено, що нарощення для одиничного періоду однаково, незалежно від того, використовується схема простих відсотків або складних.
Обґрунтуємо сказане. Справді при i> 0:
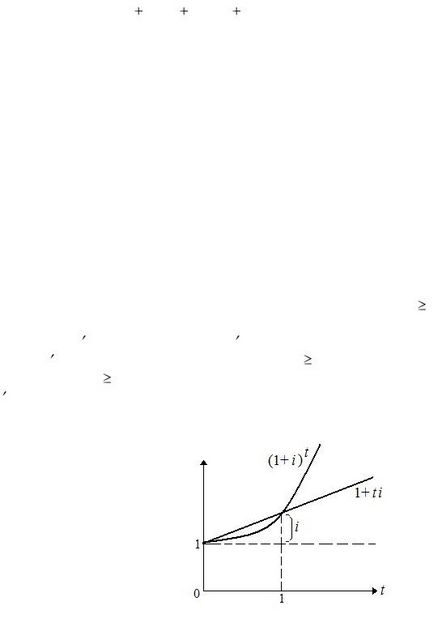
якщо t> 1, то (1+ i) t> 1+ it; якщо 0 Для доказу цього факту розглянемо функції f (t) = (1 + i) t і g (t) = 1 + it. Очевидно, f (0) = g (0), f (1) = g (1) і обидві функції зростають при t 0 не тільки по їх змістовного змістом, а й формально через позитивності їх похідних f (t) = (1+ i) t ln (1 + i) і g (t) = i. У той же час похідна другого порядку f (t) = (1 + i) t ln 2 (1 + i) є позитивною при t 0, що означає опуклість вниз функції f (t) при t 0 (тобто прискорене зростання) . При цьому функція g (t) зростає лінійно На графіку зображені функції f (t) = (1 + i) t і g (t) = 1 + it в залежності від t: Приклад. Нехай сума P = 800 нарощується за ставкою i = 8% простих і складних відсотків. Тоді наращѐнние суми такі
Для оцінки своїх перспектив кредитору та боржнику часто важливо знати, через скільки часу сума позики зростає в N раз при даній процентній ставці i. Для цього прирівняємо множник нарощення величиною N. в результаті чого отримаємо:
a) для простих відсотків 1 + ni = N. звідки n = (N-1) / i.
b) для складних відсотків (1 + i) n = N. звідки n = ln N / ln (1 + i).
Завдання 4. Розрахувати, за скільки років борг збільшиться вдвічі при ставці простих і складних відсотків, яка дорівнює 4% річних. Результати порівняти.
Рішення. За умовою завдання i = 0.04, N = 2. маємо
a) для простих відсотків n = (N-1) / i = 1 / i. звідки n = 1 / 0.04 = 25 років
b) для складних відсотків n = ln N / ln (1 + i), звідки n = ln 2 / ln (1.04) 17.67 років. Розрахунок за схемою складних відсотків швидше подвоює борг.
Деякі способи нарахування відсотків при дробовому числі років
У практиці фінансових установ при дробовому числі років t відсотки нараховуються по-різному. Розглянемо три основні способи нарахування.
1. За формулою складних відсотків: S = P (1 + i) t.
2. На основі змішаного методу, згідно з яким за ціле число років нараховуються складні відсотки, а за дробове - прості: S = P (1 + i) n (1 + bi), де t = n + b. n - ціле число років, b - дрібна частина року.
3. У ряді комерційних банків застосовується правило, згідно з яким за відрізок часу менше періоду нарахування відсотки не нараховуються, тобто
Завдання 5. Розмір позики, представленої на 27 місяців, дорівнює 100 000 р. Річна процентна ставка дорівнює 20%. Обчислити наращѐнную суму зазначеними трьома способами.
Рішення. За умовою завдання термін позики складає 2.25 року. Маємо такі розрахунки.
За 1-му способу: S I = 100 000 (1 + 0.2) 2. 2 5 150 715 р. 46 коп. За 2-му способу: S II = 100 000 (1 + 0.2) 2 (1 + 0.25 0.2) = 151 200 р. За 3-му способу: S III = 100 000 (1 + 0.2) 2 = 144 000 р.
Формули дисконтування в разі складних відсотків
При математичному дисконтуванні з формули

Якщо здійснюється дисконтування за схемою банківського (комерційного) обліку, то спочатку обмовляється облікова ставка d. 0 d <1. Она применяется не к начальной сумме, как при простой учетной ставке, а к сумме, уже дисконтированной на предыдущем промежутке времени. Размер дисконта, или учета, удерживаемого финансовым учреждением, равен
Завдання 7. Вексель на суму 20 000 р. термін платежу за яким настає через 1.5 року, врахований по складній процентній ставці 18% річних. Визначити суму, отриману власником векселя при обліку, а також відповідний дисконт.
Рішення. Тут за умовою задачі S = 20 000, n = 1.5, d = 0.18. Тоді за формулою (4) отримуємо наступні результати розрахунків:
сума, одержувана власником P = 20 000 (1 - 0.18) 1.5 14850 р. 83 коп.,
дисконт D = S - P 20 000 - 14850.83 = 5149 р. 17 коп.