Рішення задач за допомогою пропорцій

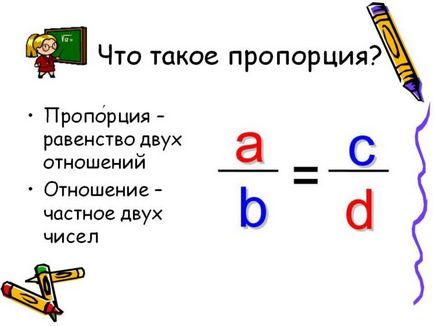
Часто на практиці доводиться вирішувати завдання, які найбільш доцільно робити за допомогою пропорцій. Якщо в умовах є дві пов'язані величини, то для вирішення таке завдання зручно приводити до рівності дробів. Дріб ще називають ставленням. Наприклад, дріб, або 2: 3 - це відношення двох до трьох. Якщо два відносини дорівнюють один одному, кажуть про пропорції. Наприклад,. Якщо обчислити значення виразів зліва і праворуч від знака «=», можна переконатися, що вони рівні між собою. Це означає, що вони є пропорцією.
Рівність словесно виражається так: «Десять відноситься до п'яти, як 30 відноситься до п'ятнадцяти», або «Десять більше п'яти в стільки ж разів, у скільки тридцять більше п'ятнадцяти». Очевидно, що в пропорції фігурують 4 числових значення - 4 члена. Якщо будь-який з них невідомий, його можна обчислити за трьома іншим членам.
Щоб обчислити x, досить помножити обидві частини на 20:
Підставами знайдене значення замість x і перевіримо правильність рішення:
Праву частину можна скоротити на 4:
Таким чином, при знайденому значенні x = 12 рівність вірно.
Помножимо обидві частини на:
Для перевірки підставимо знайдене значення замість x:
Права частина скорочується на 2:
Отже, при розрахунковому значенні x = 6 рівність вірно.
Основна властивість пропорції
Якщо a: b = c: d, то a і d є крайніми членами цієї пропорції, b і c - середніми. Основна властивість полягає в наступному: твір крайніх членів дорівнює добутку середніх: ad = bc. При записи у вигляді рівності дробів крайні і середні члени утворюють 2 діагоналі в формі хреста. І основне властивість можна заради наочності формулювати по-іншому: твори членів, що складають праву діагональ, дорівнює добутку членів, що утворюють ліву діагональ ( «правило хреста»). Щоб переконатися, що ця властивість дійсно притаманне пропорції, досить помножити обидві її частини на bd:
Скоротивши обидві частини, позбудемося знаменників і отримаємо:
Використовуючи основну властивість, можна легко і швидко знаходити невідомий член.
За основним властивості:
Перевіримо правильність рішення:
Праву частину скоротимо на 5:
Таким чином, при отриманому значенні x = 40 рівність вірно.
Пряма і зворотна залежність
Припустимо, є два змінюються параметра x і y. Причому, збільшення або зменшення будь-якого з них в деяке число раз тягне за собою таку зміну та іншого в таке ж число раз. У цьому випадку говорять про пряму залежність, або прямий пропорційності величин між собою: x прямо пропорційний величині y, y прямо пропорційний параметру x. Прямо пропорційними є такі пари як обсяг речовини і його маса, швидкість руху і пройдену відстань за деякий час, кількість працівників і обсяг роботи, який вони здатні виконати за певний час і т. Д.
Людина проходить відстань від свого будинку до тролейбусної зупинки (250 м) за 5 хвилин, до автобусної - за 7 хвилин. Яка відстань від будинку до зупинки автобуса?
Так як збільшився час, витрачений на дорогу, очевидно, що збільшилася і пройдену відстань. Причому, обидва цих параметра зросли в однакову кількість разів: Щодо першого відстані до другого дорівнює відношенню першого проміжку часу до другого. Таким чином, відстань і час на його проходження прямо пропорційні між собою. Висловимо завдання рівністю дробів і вирішимо її за допомогою основного властивості:
Відповідь: відстань до автобусної зупинки становить 350 м
Припустимо, є два змінних параметра x і y. Причому, збільшення будь-якого з них в деяке число раз призводить до зменшення іншого в той же число раз. І навпаки, зменшення будь-якого з них в будь-яке кількість разів призводить до збільшення іншого в цю ж кількість разів. Іншими словами, збільшення будь-якого параметра відповідає збільшенню іншого в зворотне число раз. У цьому випадку говорять про зворотну залежність: x обернено пропорційний y, y обернено пропорційний x.
Пливучи зі швидкістю 45 км / год, катер пройшов певний шлях за 4 год. За якийсь час він пройде цей же шлях при швидкості 40 км / год?
Так як швидкість катера зменшилася, часу на пропливаніе йому буде потрібно більше. Значить, швидкість і час обернено пропорційні один одному. Таким чином, ставлення першої швидкості до другої дорівнює відношенню другого проміжку часу до першого:
Відповідь: при швидкості 40 км / год катер пройде даний шлях за години.
Вася виконав необхідну кількість віджимань за 1 хвилину. Ваня віджимається в рази швидше. За якийсь час Ваня відіжметься необхідну кількість разів?
Оскільки Ваня віджимається швидше Васі, то часу йому буде потрібно менше. Причому, Ванін проміжок часу буде в стільки ж разів менше, у скільки разів більше його швидкість (в рази). Таким чином, час виконання однакової кількості віджимань і швидкість обернено пропорційні між собою. Позначимо час віджимань Вані як x, тоді
x = 1 хв. = = Хв
Незважаючи на наявність в умовах зворотній залежності, в даному випадку для вирішення немає сенсу використовувати рівність дробів.
