Приклад аналізу функції для побудови ескізу графіка
Приклад дослідження функції для побудови ескізу графіка.
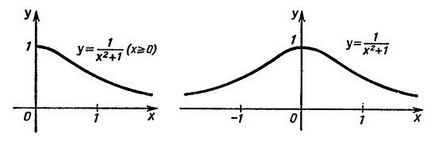
Досліджуємо функцію f (X) = 1 / (x 2 +1) і згідно з отриманими результатами намалюємо ескіз її графіка.
Спочатку знайдемо область визначення функції. Так як знаменник дробу не вернувся в нуль ні при яких значеннях x, функція визначена на всій числовій прямій - x може приймати будь-які значення. Зауважимо, що функція f (x) парна, так як f (-x) = 1 / ((- x) 2 +1) = 1 / (x 2 +1) = f (x). Так як функція парна, то достатньо її досліджувати і побудувати ескіх графіка тільки для позитивних х, а потім відобразити ескіз щодо осі ординат. Тепер знайдемо точки перетину графіка функції з координатними осями. З віссю ординат графік перетинається в точці (0; f (0)). Для нашої функції це точка (0; 1), так як f (0) = 1. Для того, щоб знайти точки перетину з віссю абсцис, треба вирішити рівняння f (x) = 0. Рівняння 1 / (x 2 +1) = 0 не має дійсних коренів, значить графік f (x) не перетинає вісь абсцис. З цього можна зробити висновок, що графік функції або весь розташовується над віссю абсцис (функція всюди позитивна), або весь під нею (функція всюди негативна). Очевидно, що дріб 1 / (x 2 +1) при будь-яких х набуває додатних значень, значить графік нашої функції весь розташовується над віссю абсцис.
При побудові графіка функції дуже корисно мати інформацію про проміжках зростання та спадання функції. Використовуючи визначення зростаючих і спадних функцій. можна визначити, що f (x) зростає на проміжку (-; 0] і убуває на проміжку [0;). Таким чином, в точці x = 0 зростання функції змінюється на спадання. f (0) = 1.
Так само зауважимо, що при необмеженому збільшенні аргументу знаменник f (x) необмежено збільшується, отже значення функції спадає до нуля (необмежено наближається до нуля). Виходячи з парності функції можна сказати, що функція поводиться точно так само і при необмежено зменшенні аргументу.
Виходячи з отриманої інформації ми можемо намалювати ескіз графіка функції, він представлений на малюнку нижче.