Побудувати ескіз графіка функції, знаючи, що - презентація 17823-15
Зразок виконання роботи >>
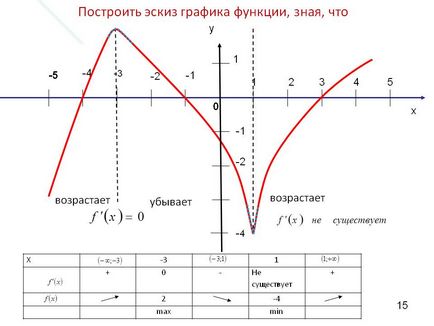
Побудувати ескіз графіка функції, знаючи, що. Зростає. Зростає. Убуває. y. 1. -4. -1. -2. 1. 2. 3. 4. 5. x. -1. -2. -3. -4. -5. 0. 15.
Слайд 15 з презентації «Застосування похідної до дослідження функцій» до уроків алгебри на тему «Похідна»
Розміри: 960 х 720 пікселів, формат: jpg. Щоб безкоштовно завантажити слайд для використання на уроці алгебри, клацніть на зображенні правою кнопкою мишки і натисніть «Зберегти зображення як. ». Завантажити всю презентацію «Застосування похідної до дослідження функцій.pptx» можна в zip-архіві розміром 1207 КБ.
похідна
«Завдання на похідну» -? F (x) = f (x) - f (x0). x0 x0 +? x. А як Ви уявляєте собі миттєву швидкість? Завдання про миттєвої швидкості. y. Як же Ви уявляєте собі миттєву швидкість. Х = х-х0. Сказане записують у вигляді. Спочатку ми визначили «територію» своїх досліджень. А л г о р і т м. Швидкість v поступово зростає.
«Дослідження функції похідною» - Пушка стріляє під кутом до горизонту. Варіант 1 А В Г Варіант2 Г Б Б. МОУ мєшковські сош Учитель математики Ковальова т.в. Функція визначена на відрізку [-4; 4]. Як пов'язані похідна і функція? Відповіді: ЗАСТОСУВАННЯ ПОХІДНОЇ ДО ДОСЛІДЖЕННЯ ФУНКЦІЇ зростання і спадання функції. ЗАВДАННЯ Пам'ятаєте розповідь про барона Мюнхгаузена?
«Похідна складної функції» - Складна функція. Правило знаходження похідної складної функції. Похідна простої функції. Похідна складної функції. Складна функція: Приклади:
«Урок похідна складної функції» - Похідна складної функції. Обчислити швидкість руху точки: а) в момент часу t; б) в момент t = 2 c. Знайдіть похідні функцій. Якщо. Брук Тейлор. Знайти диференціал функції: При яких значеннях х виконується рівність. Точка рухається прямолінійно за законом s (t) = s (t) = (s - шлях в метрах, t - час в секундах).
«Визначення похідної» - 1. Доказ: f (x +? X). Нехай u (x). v (x) і w (x) - диференціюються в деякому інтервалі (a; b) функції, С - постійна. f (x). Рівняння прямої з кутовим коефіцієнтом: За формулою бінома Ньютона маємо: Теорема. Тоді: Похідна складної функції.
Всього в темі «Похідна» 31 презентація