Побудова кореневих годографов - студопедія
У більшості випадків характеристичне рівняння досліджуваної системи представимо у вигляді
де і поліноми комплексного змінного s. - деякий параметр, який в подальшому будемо називати варійованим. (Таким параметром може служити, наприклад, передавальний коефіцієнт k розімкнутої системи).
Траєкторії, які описують коріння характеристичного рівняння на площині S при зміні параметра системи від 0 до ∞ отримали назву кореневих годографов. Побудовані кореневі годографи дозволяють обчислити, як впливає на стійкість і динамічні характеристики системи зміна змінними параметрами.
Маючи характеристичне рівняння (1) з відомими нулями входять до нього полиномов L (s) і D (s) можна приблизно побудувати на площині S кореневі годографи.
Для цього (1) переписуємо у вигляді:
З огляду на, що s - комплексна змінна, (2) можна записати у вигляді двох рівнянь: рівняння аргументів
і рівняння модулів
Уявімо і в вигляді:
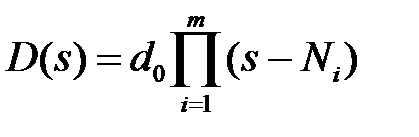
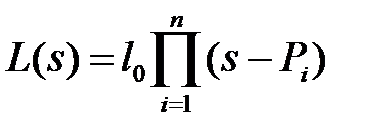
де і - коефіцієнт при s найвищого ступеня,
. - нулі поліномів і,
m і n - порядки поліномів і.
Рівняння аргументів (3) можна переписати в наступному вигляді:
З виразу (5) слід: точка s площині S належить кореневого годографа, якщо сума аргументів векторів, проведених з нулів функції
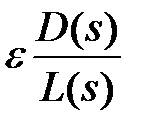
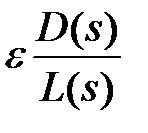
(Сказане показано на рис.1)
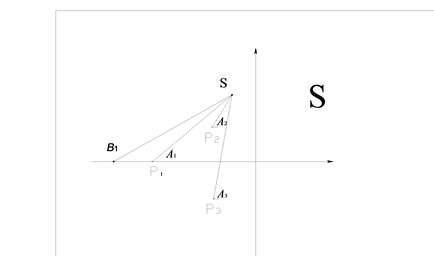
На цьому малюнку через позначені аргументи векторів, проведених з полюсів
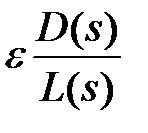
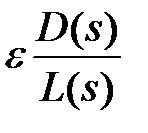
На підставі виразу (5) можна сформулювати такі основні правила побудови кореневих годографов:
1. Матеріальна вісь площин S є віссю симетрії для кореневих годографов і для асимптот кореневих годографов.
2. При зміні від 0 до ∞ кореневі годографи вийшовши з полюсів функції
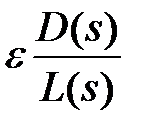
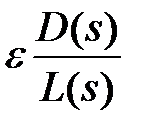
Якщо число полюсів n більше числа нулів m, то (n-m) гілок кореневого годографа підуть в нескінченність. Якщо число нулів більше числа полюсів, то (n-m) гілок кореневого годографа прийдуть з нескінченності.
3. Гілки кореневих годографов, що знаходяться в нескінченності мають асимптоти. Число асимптот одно. Асимптоти перетинаються в одній точці дійсної осі площині S, причому:
і мають кути нахилу щодо позитивного напрямку дійсної осі площині S:
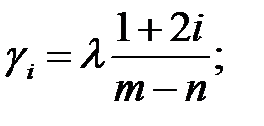
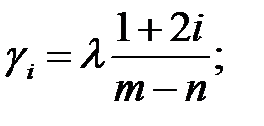
4. Точки дійсній осі площини S праворуч від яких знаходиться непарне число нулів і полюсів функції
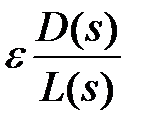
5. У деяких точках дійсній осі площини S, що належать кореневих годографом, кореневі годографи можуть, зустрівшись, розійтися, один у верхню, а інший в нижню частини площині S.
Сформульовані вище правила дозволяють наближено виконати побудову кореневих годографов.
Розглянемо деякі приклади побудови кореневих годографов.
Побудувати кореневі годографи для змінними параметрами До для замкнутої системи, якщо передавальна функція розімкнутої системи:
Рішення: Характеристичне рівняння замкнутої системи. Уявімо його у вигляді. Звідси видно, що кількість нулів дорівнює 0, а кількість полюсів дорівнює 4. Їх значення можна отримати, знайшовши корені знаменника. отримуємо

Наносимо полюса на комплексну площину. Відповідно до правила 2 всі кореневі годографи повинні піти в нескінченність. Число асимптот одно 4-0 = 4. Визначимо точку, розташовану на дійсній осі, в якій перетинаються асимптоти -7,5
Визначимо кути, які асимптоти складають з позитивним напрямком дійсної осі (правило 3).
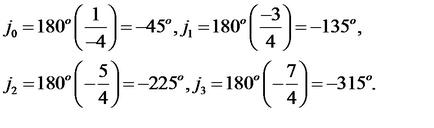
Наносимо асимптоти на комплексну площину, як показано на рис.2. На цьому ж малюнку показані кореневі годографи, які виходять з полюсів і йдуть в нескінченність, необмежено наближаючись до намальованих асимптотам.
Рішення: Характеристичне рівняння замкнутої системи має вигляд
Прирівнюючи до нуля чисельник і знаменник, отримаємо нулі і полюси кореневих годографов
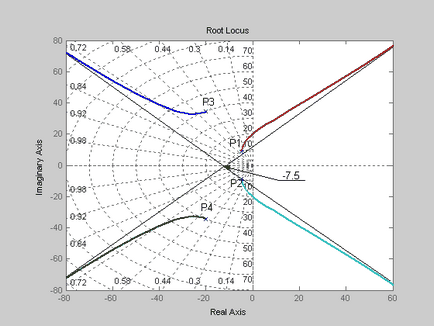
Наносимо полюса і нулі на комплексну площину, як показано на рис.2. Відповідно до правила 1, два кореневих годографа повинні закінчитися в нескінченності, крім того відповідно до правила 4 жодна з точок дійсної площини не належить кореневих годографом.
Відповідно до правила 3, кореневі годографи мають 2 асимптоти, пересічні з речової віссю в точці
Кути між асимптотами і позитивним напрямком дійсної осі дорівнюватимуть (правило 3)
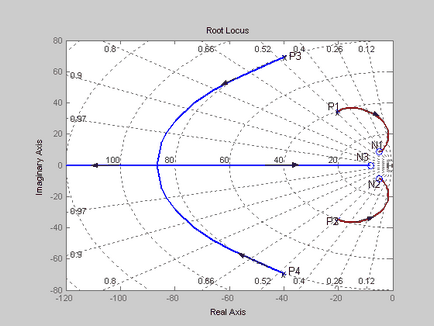
З урахуванням сказаного кореневі годографи матимуть вигляд, показаний на рис.3. Кореневі годографи вийшовши з полюсів P1 і P2 закінчаться в нулях N1 і N2. Кореневі годографи вийшовши з полюсів P3 і P4 підуть в нескінченність необмежено наближаючись до асимптотам, які перетинають речову вісь в точці -55.
Рішення: Характеристичне рівняння замкнутої системи
Уявімо його у вигляді
Нулі кореневих годографов будуть:
Полюса кореневих годографов будуть:
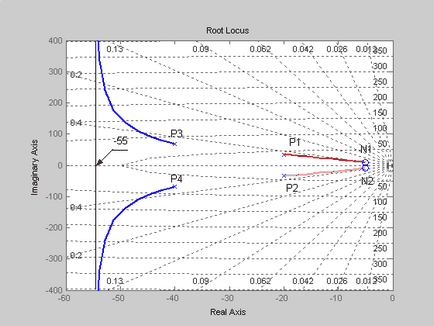
Наносимо нулі і полюси на комплексну площину, як показано на рис. 4. Відповідно до правила 4, частина дійсної осі, що лежить лівіше нуля N3 буде належати кореневих годографом, при цьому цей відрізок осі є асимптотой для годографа, який іде у нескінченність.
Кореневі годографи, побудовані у відповідності з викладеними вище правилами, зображені на тому ж малюнку. Два кореневих годографа, вийшовши з полюсів P1 і P2 прийдуть в нулі N1 і N2. Кореневі годографи, вийшовши з полюсів P3 і P4 зійдуться в одній точці на дійсній осі, що дорівнює приблизно 84 і, потім один закінчиться нулі N3. а другий піде в нескінченність.