Площі подібних фігур
Площі подібних фігур
Нехай F 'до F "- дві подібні прості фігури. З'ясуємо, як ставляться площі цих фігур. Так як фігури подібні, то існує перетворення подібності, при якому фігура F' переходить в фігуру F".
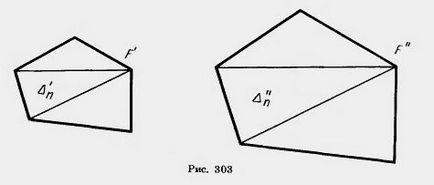
Розіб'ємо фігуру F 'на трикутники. (Рис. 303). Перетворення подібності. переводить фігуру F 'в F ", переводить ці трикутники в трикутники розбиття фігури F". Площа фігури F 'дорівнює сумі площ трикутників AU Аг, а площа фігури F "дорівнює сумі площ трикутників.
Якщо коефіцієнт подібності дорівнює k, то розміри трикутника в k разів більше відповідних розмірів трикутника. Зокрема, сторони і висоти трикутника в k разів більше відповідних сторін і висот трикутника. Звідси слідує що
Коефіцієнт подібності до дорівнює відношенню відповідних лінійних розмірів фігур F "і F '. Тому площі подібних фігур відносяться як квадрати їх відповідних лінійних розмірів.
А. В. Погорєлов, Геометрія для 7-11 класів, Підручник для загальноосвітніх установ
Збірник конспектів уроків з математики скачати. календарно-тематичне планування, підручники з усіх предметів онлайн
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.