Презентація на тему площі подібних фігур теорема
Презентація на тему: "Площі подібних фігур Теорема. Відношення площ подібних фігур дорівнює квадрату коефіцієнта подібності. Слідство. Площі подібних багатокутників відносяться." - Транскрипт:
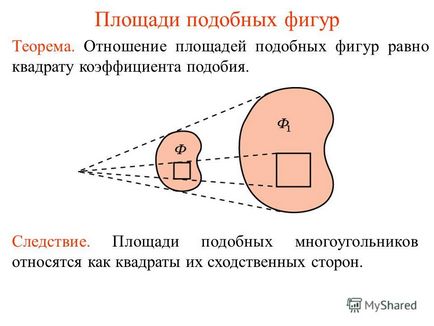
1 Площі подібних фігур Теорема. Відношення площ подібних фігур дорівнює квадрату коефіцієнта подібності. Слідство. Площі подібних багатокутників відносяться як квадрати їх подібних сторін.
2 Вправа 1 Знайдіть відношення площ двох квадратів, якщо відношення сторін цих квадратів одно: а) 2: 3; б); в) 1. 1,5. Відповідь: а) 4. 9; б) 2. 3; в) 1. 2,25.

3 Вправа 2 Як ставляться боку двох квадратів, якщо відношення площ цих квадратів одно: а) 4. 9; б) 3. 4; в) 0,5. 2? Відповідь: а) 2. 3; в) 1. 2. б). 2;

4 Вправа 3 Сторони рівносторонніх трикутників рівні 6 см і 7 см. Чому дорівнює відношення їх площ? Відповідь: 36. 49.

5 Вправа 4 Периметри двох подібних багатокутників відносяться як 1. 2. Як відносяться їх площі? Відповідь: 1. 4.

6 Вправа 5 Як зміниться площа кола, якщо його діаметр: а) збільшити в 2 рази; б) зменшити в 5 разів? Відповідь: а) Збільшиться в 4 рази; б) зменшиться в 25 разів.

7 Вправа 6 Одна зі сторін трикутника розділена на три рівні частини і через точки поділу проведено прямі, паралельні іншій стороні. Знайдіть відношення площі даного трикутника до площ трикутників, відсічених побудованими прямими. Відповідь: 9. 4. 1.

8 Вправа 7 Пряма, паралельна стороні трикутника, ділить його на дві рівновеликі частини. У якому відношенні ця пряма ділить інші сторони трикутника? Відповідь. 1.

9 Вправа 8 Площа даного багатокутника дорівнює 45 см 2. Чому дорівнює площа багатокутника, йому подібного, якщо подібні боку багатокутників рівні 15 см і 10 см? Відповідь: 20 см 2.

10 Вправа 9 Периметри двох подібних багатокутників відносяться як 3: 5. Площа більшого багатокутника дорівнює 40 м 2. Знайдіть площу другого багатокутника. Відповідь: 14,4 м 2.

11 Вправа 10 Як зміниться площа багатокутника, якщо кожна з його сторін: а) збільшиться в n раз; б) зменшиться в m раз (а величини кутів не зміняться)? Відповідь: а) Збільшиться в n 2 разів; б) зменшиться в m 2 раз.
12 Вправа 11 Периметри двох правильних n - кутників відносяться як a: b. Як ставляться їх площі? Відповідь: a 2. b 2.
13 Вправа 12 Знайдіть відношення площ правильних шестикутників, вписаного і описаного близько даної окружності. Відповідь: 3: 4.
14 Вправа 13 У колі з центром O проведена хорда AB. На радіусі OA, як на діаметрі, описана окружність. Доведіть, що площі двох сегментів, що відсікаються хордою AB від обох кіл, відносяться як 4. 1. Рішення: Зауважимо, що велика окружність виходить з малої Гомотетія з центром в точці A і коефіцієнтом 2. При цій гомотетии сегмент малого кола переходить в сегмент великий окружності. Отже, ставлення їх площ дорівнює 4. 1.
15 Вправа 14 Два кола, радіусів R і r стосуються внутрішнім чином. Через точку дотику проведена хорда, яка відсікає від зовнішньої окружності сегмент площі S. Знайдіть площу сегмента, який відсікається цією хордою від внутрішньої окружності. відповідь:
16 Вправа 15 Фігура Ф 'отримана з фігури Ф стисненням до прямої a в k раз. Чому дорівнює відношення площ фігур Ф 'і Ф? Відповідь: 1. k.
17 Вправа 16 На малюнку зображена фігура Ф, отримана стисненням кола радіуса R в 2 рази. Чому дорівнює її площа? відповідь: