площі многокутників
Можна сказати, що площа багатокутника - це величина, що позначає частину площині, яку займає даний багатокутник. За одиницю виміру площі приймають площу квадрата зі стороною \ (1 \) см, \ (1 \) мм і т.д. (Одиничний квадрат). Тоді площа буде вимірюватися в см \ (^ 2 \). мм \ (^ 2 \) відповідно.
Іншими словами, можна сказати, що площа фігури - це величина, чисельне значення якої показує, скільки раз одиничний квадрат вміщується в даній фігурі.
1. Площа будь-якого багатокутника - величина позитивна.
2. Рівні багатокутники мають рівні площі.
3. Якщо багатокутник складений з кількох багатокутників, то його площа дорівнює сумі площ цих багатокутників.
4. Площа квадрата зі стороною \ (a \) дорівнює \ (a ^ 2 \).
Теорема: площа прямокутника
Площа прямокутника зі сторонами \ (a \) і \ (b \) дорівнює \ (S = ab \).
Добудуємо прямокутник \ (ABCD \) до квадрата зі стороною \ (a + b \). як показано на малюнку:

Даний квадрат складається з прямокутника \ (ABCD \). ще одного рівного йому прямокутника і двох квадратів зі сторонами \ (a \) і \ (b \). Таким чином,
Висота паралелограма - це перпендикуляр, проведений з вершини паралелограма до сторони (або до продовження боку), що не містить цю вершину.
Наприклад, висота \ (BK \) падає на бік \ (AD \). а висота \ (BH \) - на продовження боку \ (CD \):
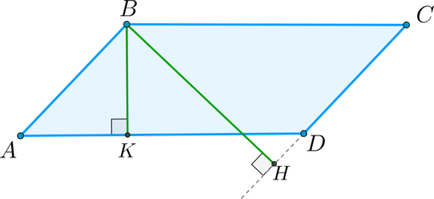
Теорема: площа паралелограма
Площа паралелограма дорівнює добутку висоти і сторони, до якої проведена ця висота.
Проведемо перпендикуляри \ (AB '\) і \ (DC' \). як показано на малюнку. Зауважимо, що ці перпендикуляри рівні висоті паралелограма \ (ABCD \).

Тоді \ (AB'C'D \) - прямокутник, отже, \ (S_ = AB '\ cdot AD \).
Зауважимо, що прямокутні трикутники \ (ABB '\) і \ (DCC' \) рівні. Таким чином,
Будемо називати сторону, до якої в трикутнику проведена висота, підставою трикутника.
Площа трикутника дорівнює половині твори його заснування на висоту, проведену до цієї підстави.
Нехай \ (S \) - площа трикутника \ (ABC \). Приймемо сторону \ (AB \) за основу трикутника і проведемо висоту \ (CH \). Доведемо, що \ [S = \ dfracAB \ cdot CH. \] Добудуємо трикутник \ (ABC \) до паралелограма \ (ABDC \) так, як показано на малюнку:
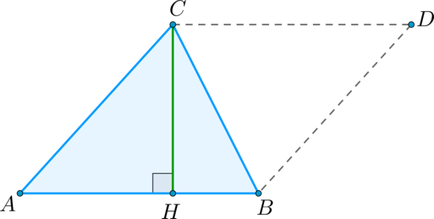
Трикутники \ (ABC \) і \ (DCB \) рівні за трьома сторонами (\ (BC \) - їх загальна сторона, \ (AB = CD \) і \ (AC = BD \) як протилежні сторони паралелограма \ (ABDC \ )), тому їх площі рівні. Отже, площа \ (S \) трикутника \ (ABC \) дорівнює половині площі паралелограма \ (ABDC \). тобто \ (S = \ dfracAB \ cdot CH \).
Якщо два трикутника \ (\ triangle ABC \) і \ (\ triangle A_1B_1C_1 \) мають рівні висоти, то їх площі відносяться як підстави, до яких ці висоти проведені.
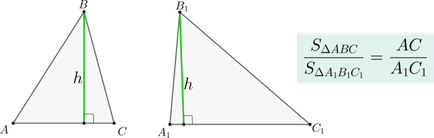
Медіана трикутника ділить його на два трикутники, рівних за площею.
Якщо два трикутника \ (\ triangle ABC \) і \ (\ triangle A_2B_2C_2 \) мають по рівному кутку, то їх площі відносяться як твори сторін, які складають цей кут.
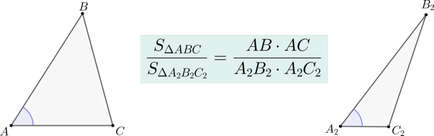
Нехай \ (\ angle A = \ angle A_2 \). Сумісний ці кути так, як показано на малюнку (точка \ (A \) поєдналася з точкою \ (A_2 \)):
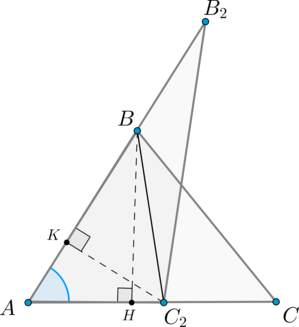
Проведемо висоти \ (BH \) і \ (C_2K \).
Трикутники \ (AB_2C_2 \) і \ (ABC_2 \) мають однакову висоту \ (C_2K \). отже: \ [\ dfrac >> = \ dfrac \]
Трикутники \ (ABC_2 \) і \ (ABC \) мають однакову висоту \ (BH \). отже: \ [\ dfrac >> = \ dfrac \]
У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів:

Вірно і зворотне: якщо в трикутнику квадрат довжини одного боку дорівнює сумі квадратів довжин інших двох сторін, то такий трикутник прямокутний.
Площа прямокутного трикутника дорівнює половині твори катетів.
Теорема: формула Герона
Нехай \ (p \) - напівпериметр трикутника, \ (a \). \ (B \). \ (C \) - довжини його сторін, тоді його площа дорівнює \ [S _ = \ sqrt \]Оскільки ромб є паралелограма, то для нього вірна та ж формула, тобто площа ромба дорівнює добутку висоти і сторони, до якої проведена ця висота.
Площа опуклого чотирикутника, діагоналі якого перпендикулярні, дорівнює половині твори діагоналей.
Розглянемо чотирикутник \ (ABCD \). Позначимо \ (AO = a, CO = b, BO = x, DO = y \):
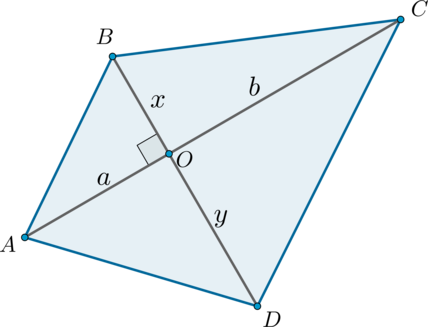
Зауважимо, що даний чотирикутник складено з чотирьох прямокутних трикутників, отже, його площа дорівнює сумі площ цих трикутників:
\ (\ Begin S _ = \ frac12ax + \ frac12xb + \ frac12by + \ frac12ay = \ frac12 (ax + xb + by + ay) = \\ \ frac12 ((a + b) x + (a + b) y) = \ frac12 (a + b) (x + y) \ end \)
Слідство: площа ромба
Площа ромба дорівнює половині твори його діагоналей: \ [S _> = \ dfrac12 d_1 \ cdot d_2 \]
Висота трапеції - це перпендикуляр, проведений з вершини одного підстави до іншого підставі.
Теорема: площа трапеції
Площа трапеції дорівнює добутку напівсуми підстав на висоту.
Розглянемо трапецію \ (ABCD \) з підставами \ (BC \) і \ (AD \). Проведемо \ (CD '\ parallel AB \). як показано на малюнку:
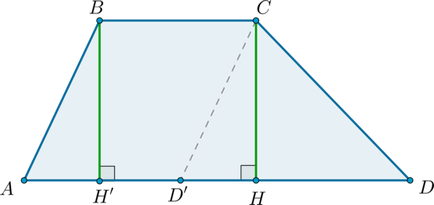
Тоді \ (ABCD '\) - паралелограм.
Проведемо також \ (BH '\ perp AD, CH \ perp AD \) (\ (BH' = CH \) - висоти трапеції).
Тоді \ (S_ = BH '\ cdot AD' = BH '\ cdot BC, \ quad S _ = \ dfrac12CH \ cdot D'D \)
Оскільки трапеція складається з паралелограма \ (ABCD '\) і трикутника \ (CDD' \). то її площа дорівнює сумі площ паралелограма і трикутника, тобто:
\ [S_ = S_ + S_ = BH '\ cdot BC + \ dfrac12CH \ cdot D'D = \ dfrac12CH \ left (2BC + D'D \ right) = \] \ [= \ dfrac12 CH \ left (BC + AD' + D'D \ right) = \ dfrac12 CH \ left (BC + AD \ right) \]