Персональний сайт - функції y sin x, y cos x, y mf (x), y f (kx), y tg x, y ctg x
Далі складемо графік. Вийде полуволна, найвища точка якої (π / 2; 1). Це графік функції y = sin x на відрізку [0; π]. Додамо до збудованого графіком симетричну півхвилю (симетричну відносно початку координат, тобто на відрізку -π). Гребінь цієї напівхвилі - під віссю x з координатами (-1; -1). В результаті вийде хвиля. Це графік функції y = sin x на відрізку [-π; π].
Можна продовжити хвилю, побудувавши її і на відрізку [π; 3π], [π; 5π], [π; 7π] і т.д. На всіх цих відрізках графік функції буде виглядати так само, як на відрізку [-π; π]. Вийде безперервна хвиляста лінія з однаковими хвилями.
Графіком функції є синусоїда (її іноді називають косинусоид).
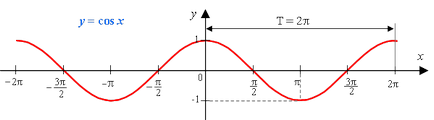
1) Область визначення функції - множина дійсних чисел.
2) Область значень функції - відрізок [-1; 1]
3) Це парна функція.
4) Це безперервна функція.
5) Координати точок перетину графіка:
- з віссю абсцис: (π / 2 + πn; 0),
- з віссю ординат: (0; 1).
6) На відрізку [0; π] функція спадає, на відрізку [π; 2π] - зростає.
7) На проміжках [-π / 2 + 2πn; π / 2 + 2πn] функція набуває додатних значень.
На проміжках [π / 2 + 2πn; 3π / 2 + 2πn] функція набуває від'ємних значень.
8) Проміжки зростання: [-π + 2πn; 2πn].
Проміжки спадання: [2πn; π + 2πn];
9) Точки мінімуму функції: π + 2πn.
Точки максимуму функції: 2πn.
10) Функція обмежена зверху і знизу. Найменше значення функції -1,
найбільше значення 1.
11) Це періодична функція з періодом 2π (Т = 2π)
Візьмемо попередню функцію y = cos x. Як ви вже знаєте, її графіком є синусоїда. Якщо ми помножимо косинус цієї функції на певне число m, то хвиля розтягнеться від осі x (або стиснеться, в залежності від величини m).
Ця нова хвиля і буде графіком функції y = mf (x), де m - будь-яке дійсне число.
Таким чином, функція y = mf (x) - це звична нам функція y = f (x), помножена на m.
Виконуючи розтягнення або стиснення, можна спочатку побудувати лише одну півхвилю синусоїди, а потім вже добудувати весь графік.
Якщо функція y = mf (x) призводить до розтягування синусоїди від осі x або стиску до осі x. то функція y = f (kx) призводить до розтягування від осі y або стиску до осі y.
Причому k - будь-яке дійсне число.
Складаючи графік цієї функції, можна спочатку побудувати одну півхвилю синусоїди, а по ній добудувати потім весь графік.
Графіком функції y = tg x є тангенсоіда.
Досить побудувати частина графіка на проміжку від 0 до π / 2, а потім можна симетрично продовжити її на проміжку від 0 до 3π / 2.
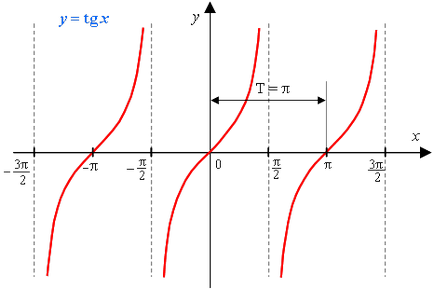
1) Область визначення функції - множина всіх дійсних чисел, крім чисел виду
x = π / 2 + πk, де k - будь-яке ціле число.
Це означає, що на графіку функції немає точки, що належить прямій x = π / 2,
або прямий x = 3π / 2, або прямий x = 5π / 2, або прямий x = -π / 2 і т.д.
2) Область значень функції (-∞; + ∞)
3) Це непарна функція.
4) Це безперервна функція на інтервалі (-π / 2; π / 2).
5) Це періодична функція з основним періодом π (Т = π)
6) Функція зростає на інтервалі (-π / 2; π / 2).
7) Функція не обмежена ні зверху, ні знизу. Не має ні найменшого, ні найбільшого значень.
Графіком функції y = ctg x також є тангенсоіда (її іноді називають котангенсоідой).
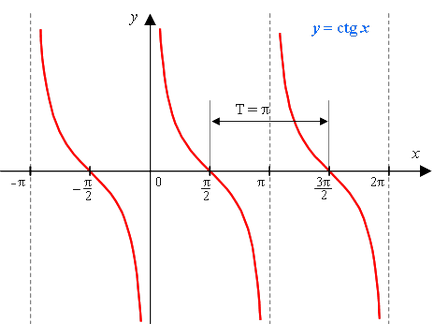
1) Область визначення функції - множина всіх дійсних чисел, крім чисел виду
x = πk, де k - будь-яке ціле число.
2) Область значень функції (-∞; + ∞)
3) Це непарна функція.
4) Це безперервна функція.
5) Це періодична функція з основним періодом π (Т = π)
6) Функція убуває в проміжку (πk; π + πk), де k - будь-яке ціле число.
7) Функція не обмежена ні зверху, ні знизу. Не має ні найменшого, ні найбільшого значень.