Перетин площиною призми, піраміди, циліндра і конуса - студопедія
СЕЧЕНИЕ геометричних ТЕЛ площині
У завданнях на побудову усічений-них геометричних тіл можна виокрем-лити наступні завдання: 1) побудова усіченого тіла в системі трьох площин проекцій; 2) визначення дійсної величини фігури перерізу; 3) побудова розгортки усіченого тіла і 4) креслення його аксони-метричної проекції. Нижче помеще-ни рекомендації щодо вирішення кожної з перерахованих завдань.
Спочатку по положенню січної площини визначають вид фігури перетину і в залежності від форми гео-метричного тіла вибирають прийом побудови проекцій перетину. В заду-пах січні площині займають проецирующее положення, тому одна проекція перетину задається. Ні-дістають проекції фігури перерізу призми або піраміди будують по точ-кам перетину їх ребер із заданою площиною. Якщо ж площина пере-Сека поверхню обертання по ле-кальной кривої, то починають з визначення її характерних точок.
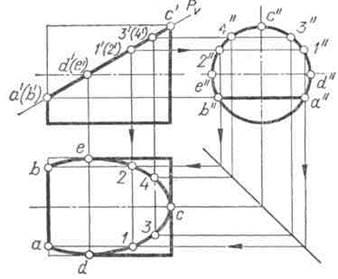
Наприклад, фронтально проектує площину Р (рис. 106) перетинає циліндр по які-повного еліпсу. Його характерними точками є: 1) А і В - точки, що належать лінії перетину площини Р з підставою циліндра; 2) С - кінець великої осі еліпса; 3) D і Е - кінці малої осі еліпса і вони ж точки, що лежать на нарисових утворюють ци-Ліндрен Послідовність знаходження точок еліпса вказана стрілками на прикладі проме-жуточних точок 1 і 2.
Натуральну величину фігури січі-ня визначають за допомогою способу зміни площин проекцій або обертання. Якщо застосовують спосіб зміни площин проекцій, то додаткову площину задають паралельно січної площини. Додаткову площину суміщають з основною площиною проекцій так, щоб нова проекція розтину не наклалася на наявні проекції. З використанням методу обертання вісь обертання доцільно распола-гать в січної площини і на неко-тором відстані від тіла.
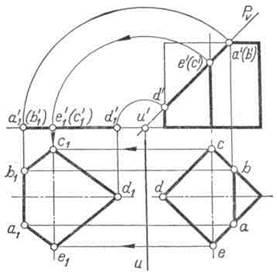
Для прикладу показано положення осі вра-щення U (рис. 107) при визначенні істинної величини перетину чотирикутної призми фронтально проецирующей площиною Р.
Побудова розгортки усіченого тіла починають з креслення розгортки його повної бічної поверхонь-сти. Далі на неї наносять лінії перетину і прилаштовують до неї інші частини розгортки - підстави і фігуру перерізу. Якщо будь-які елементи, необхідні для побудови разверт-ки, на проекціях спотворені, то перед-ньо визначають їхню справжню величину.
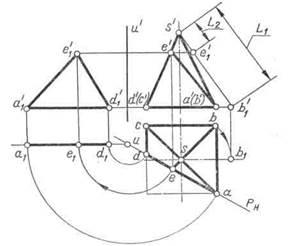
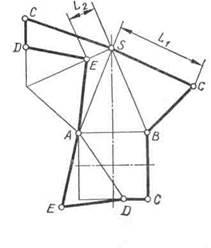
Наприклад, для побудови розгортки пра-вільной усіченої чотирикутної піраміди (рис. 108) необхідно визначити справжню ве-личину фігури перетину - трикутника ADE і довжину одного з її бічних ребер, наприклад ребра SB. Для визначення дійсної величини цих елементів їх повертають до положення, паралельного площині V. Трикутник ADE повер-нут навколо осі U, а ребро SB - навколо висо-ти піраміди. Далі будують розгортку відповідно до рекомендацій в наступному порядку: задають положення вершини S; викреслюють розгортку повної бічної поверхні піраміди; наносять на неї лінії перетину DE і AE за допомогою від-різко SE = = s 'e'1 = L2 і DC = dc; прилаштовують до ребру підстави АВ фігуру усіченого підстави- чотирикутник ABCD = abcd і до його стороні AD - трикутник ADE = a'1 e'1 d'1.
Усічені тіла на аксонометріче-ської проекції спочатку викреслюють цілими. Далі зображують проекцію перетину і контурними лініями обво-дять усічену частину тіла.
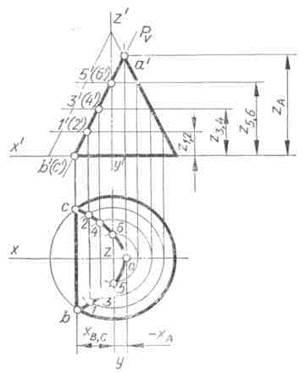
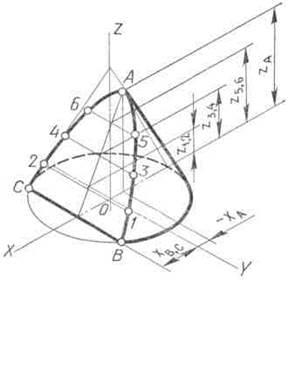
Для прикладу на рис. 109 викреслена з-метрична проекція конуса, зрізаного фронтально проецирующей площиною Р по параболі. Параболу на ізометричної проекції починають будувати з її вершини А. Цю точку отримують за допомогою координати-хА. Проекції нижніх точок параболи В і С будують по координаті хВ, С. Поєднавши точку А з серединою відрізка ВС, отримують проек-цію осі симетрії параболи. Для построе-ня її проміжних точок відкладають по осі конуса від його заснування відрізки, рівні координатами z1,2. z3,1. z5,6. Через кінці від-викладених відрізків проводять прямі, па-паралельно осі координат X, до перетину з віссю симетрії параболи. Через отриманий-ні точки проводять хорди параболи, які паралельні її нижній хорді ВС. Довжину кожної хорди заміряють на горизонтальній проекції усіченого конуса і відкладають на відповідній хорді ізометричної проекції.
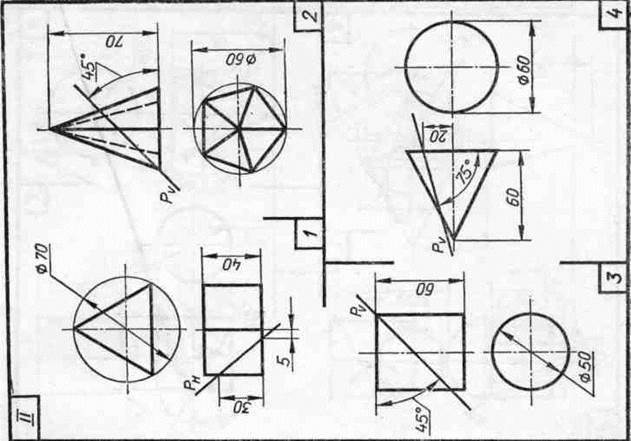
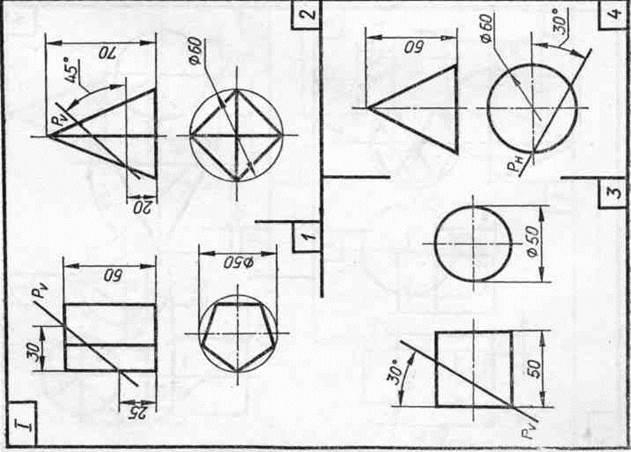
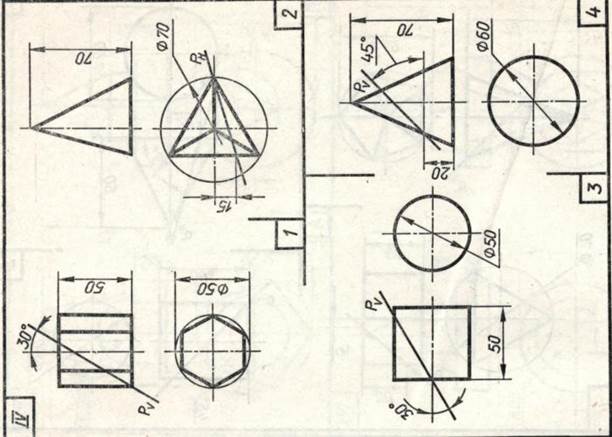
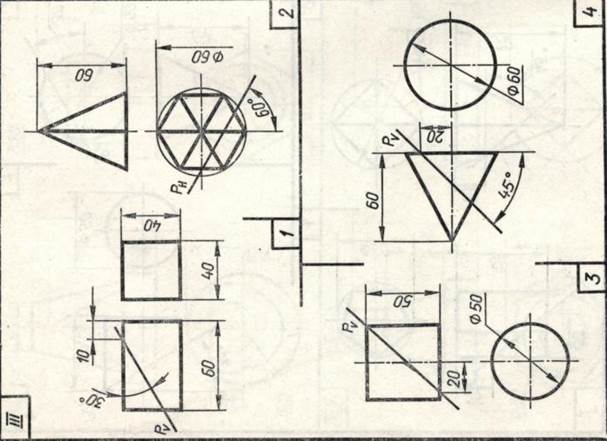
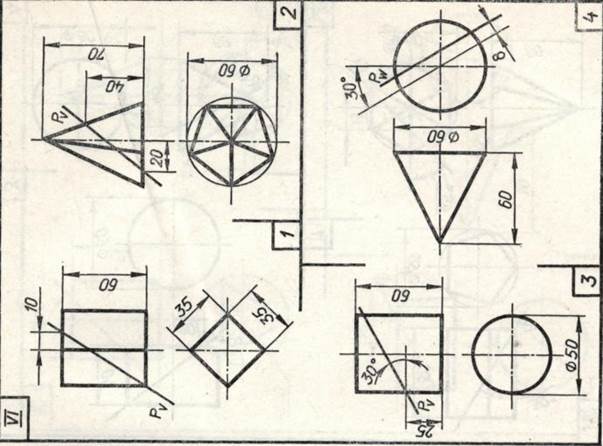
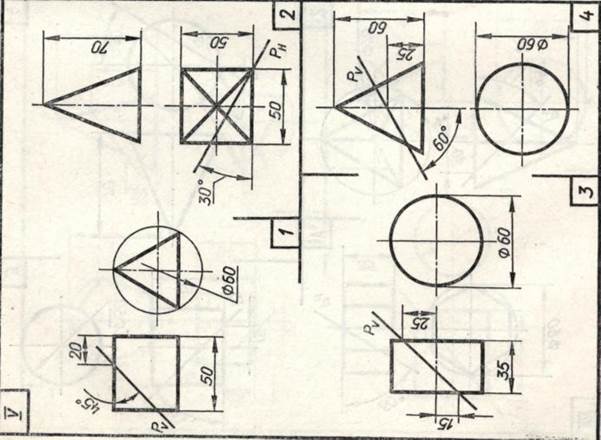
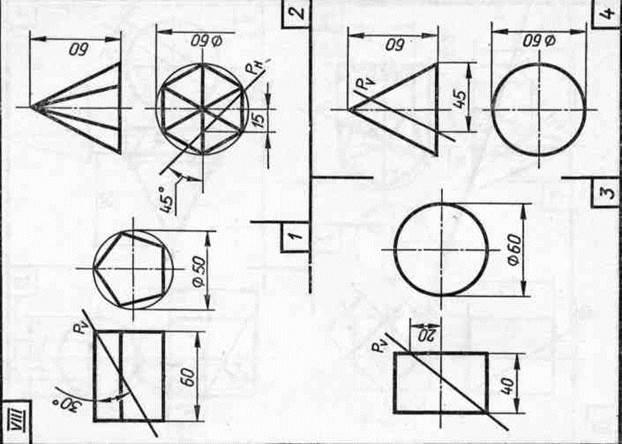
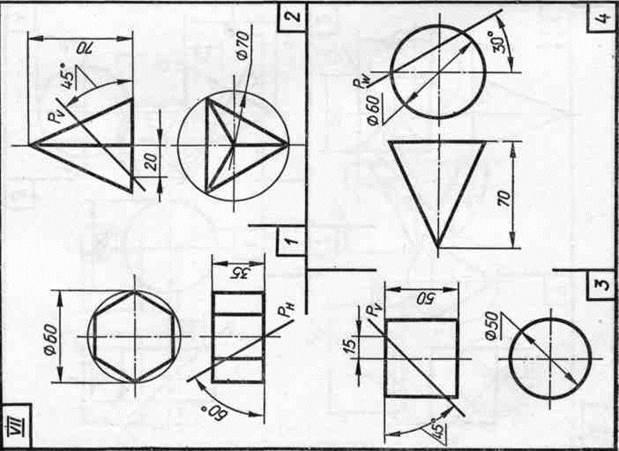
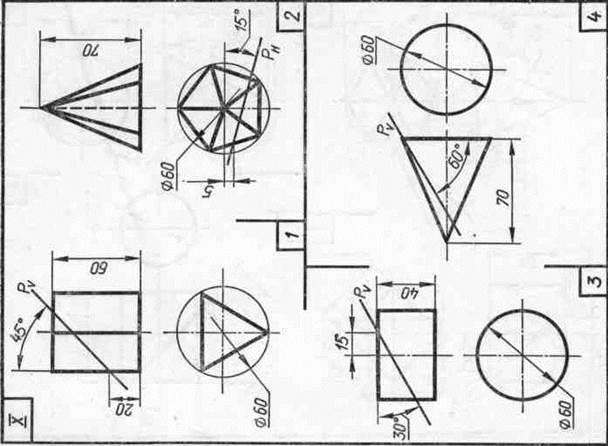
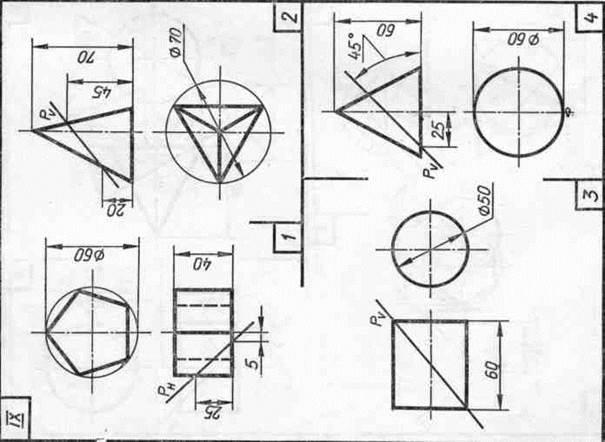
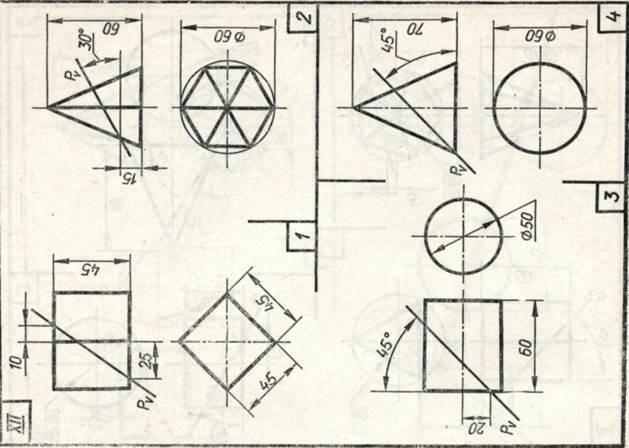
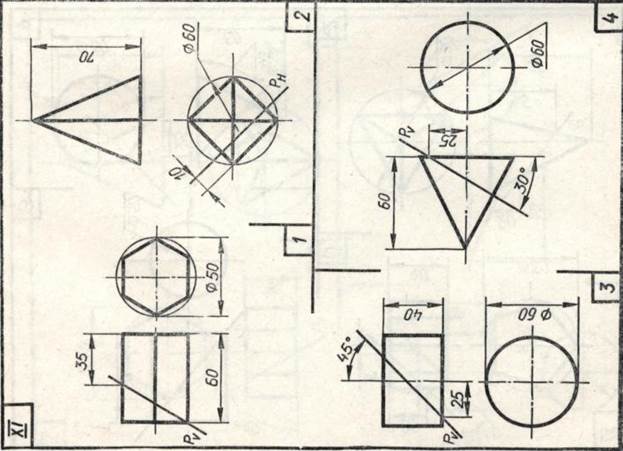
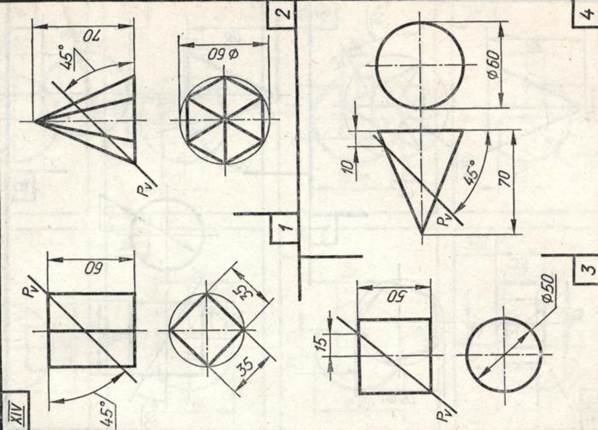
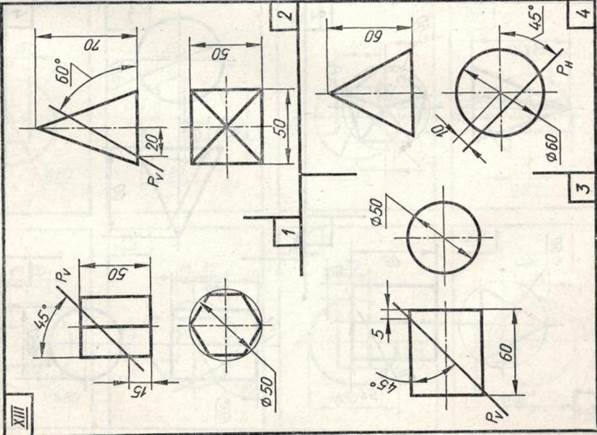
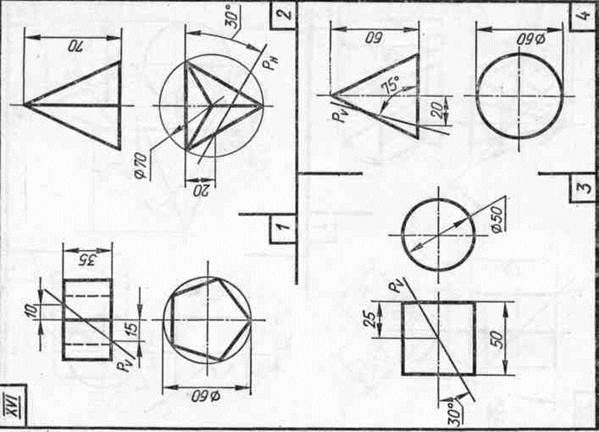
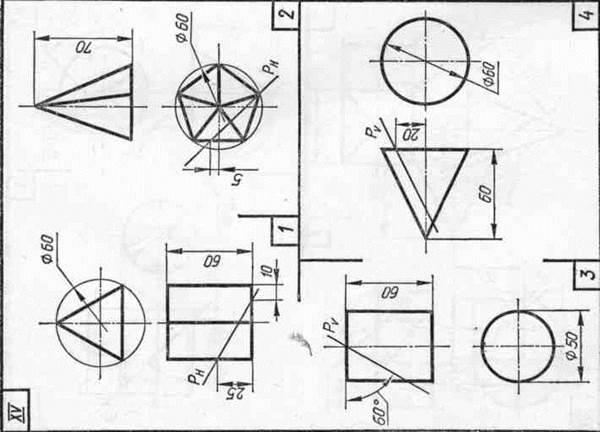
Завдання 23. Усічені геомет-рические тіла. Побудувати задані усічені геометричні тіла (приз-му, піраміду, циліндр, конус) в сі-стем трьох площин проекцій, визна-ділити справжні величини фігур се-чення, викреслити розгортки усічених тіл і їх аксонометричні проекції. Вид аксонометрической проекції вка-зан в табл. 13.
Прямокутна ізометрична проекція
Прямокутна діметріческая проекція
Зображення кожного геометричний-ського тіла розташовують на аркуші фор-мату A3.
Зразки виконаного завдання з різними варіантами оформлення приведені на рис. 110-113.
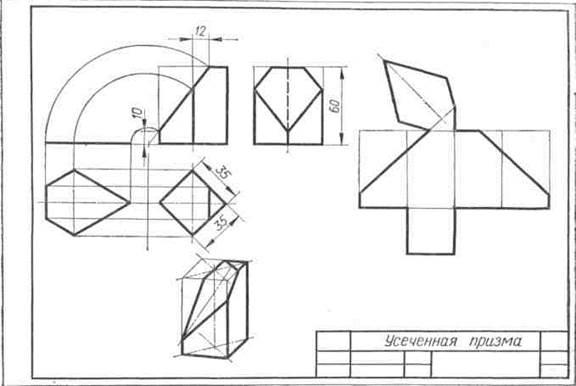
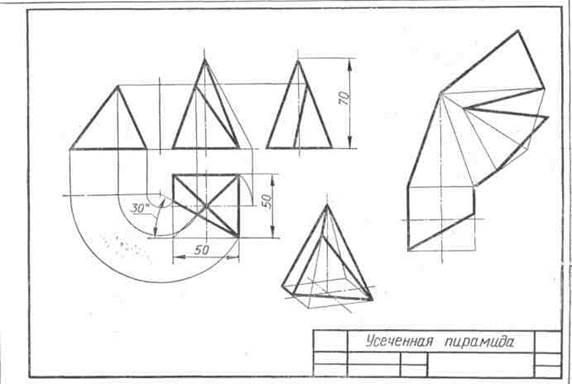
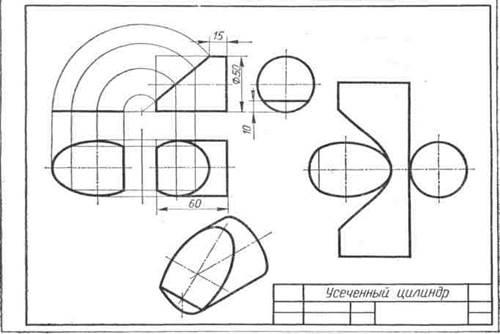
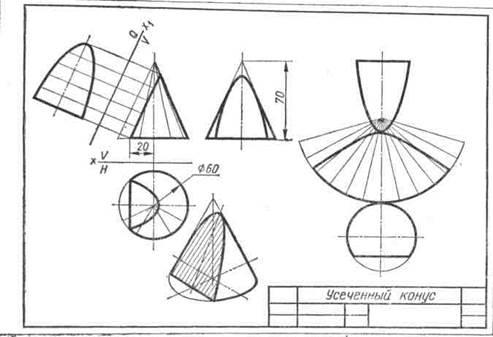
Роботу над завданням слід на-чину з компонування креслення, яка досить трудомістка через великої кількості зображень. Габарити горизонтальної, фронтальної, про-фильной і аксонометрической проек-ций тіла підраховують по заданих проекцій. Розміри перетину і раз-вертка визначають приблизно або роблять на чернетці потрібні по-будови.