Магнітне поле соленоїда і тороїда
Соленоїд є провід, щільно навитий на циліндричний каркас. Лінії напруженості магнітного поля соленоїда мають вигляд, представлений на рис. 3.22 і 3.23.
Формулу (3.48) можна застосувати для обчислення магнітної індукції поля всередині нескінченного соленоїда. В цьому випадку соленоїд зручно розглядати, як систему кругових витків із загальною прямий віссю. Силові лінії поля всередині соленоїда паралельні його осі, а поле соленоїда однорідне. Для обчислення циркуляції візьмемо прямокутний контур a-b-c-d (рис. 3.22).
Мал. 3.22 Магнітне поле всередині соленоїда
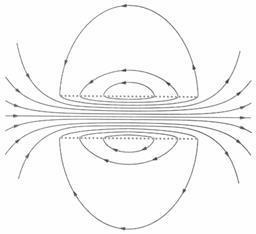
Мал. 3.23 Магнітне поле соленоїда
Циркуляцію вектора В у цій контуру можна представити у вигляді
так як на цих ділянках. Оскільки, соленоїд нескінченно довгий, силові лінії, які проходять всередині нього, починаються в нескінченності і йдуть в нескінченність. Тому магнітне поле зовні соленоїда відсутня. Тому
Тоді циркуляція вектора по замкнутому контуру запишеться у вигляді
де в # 8209; величина магнітної індукції поля в точках розташування відрізка a # 8209; b. а l # 8209; довжина цього відрізка.
Сумарний струм, що охоплюється контуром, Iполн = nlI. де # 8209; число витків на одиницю довжини соленоїда, I # 8209; сила струму в соленоїді. Тоді, згідно з (3.51):
звідки в остаточному вигляді виходить
Таким чином, поле нескінченного соленоїда однорідне, зосереджено цілком всередині соленоїда, а силові лінії вектора магнітної індукції паралельні осі соленоїда.
Якщо подумки розділити нескінченний соленоїд деякої площиною перпендикулярній осі соленоїда, то магнітне поле в точках цієї площини буде створюватися в однаковій мірі обома половинками соленоїда. Якщо тепер прибрати половину соленоїда, то у кінця напівнескінченного соленоїда В дорівнюватиме:
Практично, якщо довжина соленоїда значно більше його діаметра, то формула (3.53) справедлива для середньої частини соленоїда, а формула (3.54) для точок поблизу кінців.
Таким чином, магнітне поле зменшується до краю. Подібний крайової ефект відсутній у соленоїда, звитого в кільце, так званого тороида. Його головна особливість полягає в тому, що все магнітне поле зосереджено всередині тороїда. Лінії вектора магнітної індукції є замкнуті концентричні кола (рис. 3.24). Вибираючи одну з таких кіл за контур обходу, і, застосовуючи теорему про циркуляцію, легко довести, що за умови виходить така ж формула, що і для нескінченно довгого соленоїда
У цьому випадку поле однорідно в кожному з перетинів тороида. Але в різних перетинах направлено різному, і має сенс говорити про однорідність поля в межах всього тороида тільки умовно, маючи на увазі тільки модуль вектора.
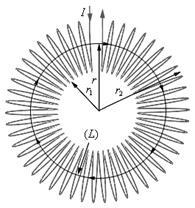
Мал. 3.24 Поле тороїда
Використовуючи теорему повного струму, можна отримати індукцію магнітного поля на осі тороїда, що має магнітний сердечник (рис. 3.24)
де - магнітна проникність сердечника; - число витків, намотаних на тороид; - радіус центральної лінії тороїда.