Магнітне поле соленоїда і тороїда - студопедія

Соленоїд представляє циліндричний каркас, на який намотані витки дроту. Розглянемо нескінченно довгий соленоїд, тобто соленоїд у якого. >> d. де. - довжина, d - діаметр соленоїда. Усередині такого соленоїда магнітне поле є однорідним. Однорідним називається поле, силові лінії якого паралельні і густота їх постійна.

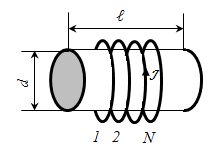
Застосуємо закон повного струму для обчислення напруженості магнітного поля соленоїда. Уявімо контур L. за яким розглядається циркуляція вектора. що складається з чотирьох пов'язаних ділянок 1-2; 2-3; 3-4; 4-1. Тоді циркуляція вектора по обраному нами контуру L буде дорівнює

;

. тому і, отже, ,

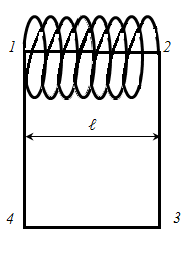
. тому ми вибрали ділянку 3-4 досить далеко від соленоїда і можна вважати, що поле далеко від соленоїда дорівнює нулю,

. тому і, отже, .

L охвативаетN струмів, де N - число витків соленоїда, тоді за законом повного струму

;

- магнітне поле нескінченно довгого соленоїда

n - щільність намотування - число витків на одиницю довжини.

Напруженість поля всередині соленоїда дорівнює числу витків, що припадають на одиницю довжини соленоїда, помноженому на силу струму.

Тороид - тор, з намотаним на нього витками дроту. На відміну від соленоїда, у якого магнітне поле є як всередині, так і зовні, у тороида магнітне поле повністю зосереджено всередині витків, тобто немає розсіювання енергії магнітного поля.

- магнітне поле тороїда.

Схожі статті

Попередня ◈ Наступна