Магнітне поле нескінченно довгого соленоїда
Соленоїд - це дротяна котушка циліндричної форми. Його можна уявити собі як безліч складених в стопку кругових витків зі струмом. Силові лінії магнітного поля, створюваного електрич-струмом в соленоїді, показані на рис. 6.6. Як видно з цього малюнка, всередині соленоїда силові лінії майже прямі. Чим довжин-неї соленоїд, тобто чим більше його довжина в порівнянні з його радіусом, тим менше кривизна силових ліній всередині соленоїда. В такому випадку вектор В магнітної індукції поля всередині соленоїда буде спрямований паралельно його осі. Причому так, що його напрямок буде пов'язано з напрямком струму в соленоїді правилом правого гвинта. Направимо вісь х вздовж осі соленоїда. При цьому проекція вектора магнітної індукції на вісь х буде дорівнює його модулю, а всі інші його проекції будуть дорівнюють нулю:
Підставами ці проекції вектора В в рівняння (6.12). отримаємо
З цієї рівності випливає, що всередині соленоїда вектор магнітної індукції не тільки зберігає свій напрямок, але його модуль тут усюди однаковий. Таким чином, приходимо до висновку, що всередині довжин-ного соленоїда магнітне поле є однорідним.
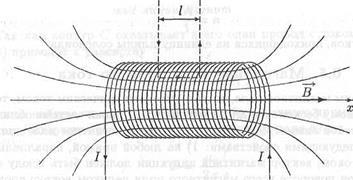
Мал. 6.6. Магнітне поле соленоїда
Знайдемо модуль вектора магнітної індукції поля всередині соленоїда за допомогою теореми (6.8) про циркуляцію цього вектора. Як кон-туру С, за яким будемо обчислювати циркуляцію вектора магнітної індукції, виберемо ламану лінію, зображену пунктиром на рис. 6.6. Відрізок цієї лінії довжиною l знаходиться всередині соленоїда і Совпа-дає з одного з силових ліній магнітного поля. Дві перпендикулярні цьому відрізку прямі починаються на його кінцях і йдуть в бесконеч-ність. У всіх точках цих прямих вектор магнітної індукції або перпендикулярний їм (всередині соленоїда), або дорівнює нулю (поза соленоїдом). Тому скалярний твір Вdl в цих точках дорівнює нулю. Таким чином, циркуляція магнітної індукції з даного контуру С буде дорівнює інтегралу по відрізку силової лінії довжиною l. З урахуванням того, що модуль вектора магнітної індукції є постійна величина матимемо
Нехай число витків соленоїда, охоплених контуром С, так само N. При цьому сума струмів, які охоплюються контуром, буде дорівнює NI, де I - сила струму в одному витку соленоїда. Теорема (6.8) приводить до рівності
з якого знайдемо магнітну індукцію поля в соленоїді:
n-число витків, що припадають на одиницю довжини соленоїда.
Магнітне поле прямого струму
Розглянемо магнітне поле, створюване електричним струмом, теку-щим по тонкому нескінченно довгому дроту. Така система має циліндричної симетрією. Внаслідок цього магнітне поле повинно мати наступні властивості:
1) на будь-який прямий, паралельної проводу зі струмом, вектор магнітної індукції повинен бути всюди оди-НАКів;
2) при повороті всього магнітного поля цілком навколо дроти воно не змінюється. В такому випадку силовими лініями магнітного поля повинні бути окружності, центри яких лежать на осі проводу з то-ком (рис, 6.7), а вектор В на будь-який з цих кіл всюди має один і той же модуль.
За допомогою теореми (6.8) про циркуляцію вектора магнітної Індуктори ції знайдемо модуль цього вектора. З цією метою обчислимо циркуляцію магнітної індукції по одній з силових ліній С, радіус якої ра-вен а. Так як вектор В є дотичним до силової лінії, він коллінеарен векторному елементу dl цієї лінії. Тому
де В - модуль вектора магнітної індукції, який, як було сказано, усюди на окружності З один і той же. Винесемо В за знак інтеграла. Після інтегрування матимемо
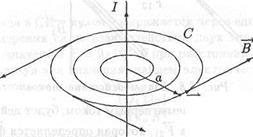
Мал. 6.7. Силові лінії магнітного поля прямого струми
Так як контур С охоплює всього один дріт зі струмом I, теорема (6.8) приводить до рівності
Звідси знайдемо, що на відстані а від нескінченного прямого проводу з струмом I індукція створюваного їм магнітного поля буде
Як видно з рис. 6.7, напрямок вектора В і напрямок струму I пов'язані правилом правого гвинта. У тому, що це дійсно так, неважко переконатися за допомогою закону Біо - Савара - Лапласа.
Розглянемо два тонких паралельних один одному прямих дроти з струмами I1 і I2 (рис. 6.8.). Якщо відстань R між проводами багато менше їх довжини, то магнітну індукцію поля, що створюється першим проводом на цій відстані, можна знайти за формулою (6.15):
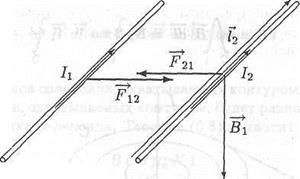
Мал. 6.8. взаємодія струмів
Магнітне поле, створюване першим струмом, буде діяти на вто-рій провід з силою Ампера F21, яка визначається формулою (5.8):
де l2 - вектор, довжина якого дорівнює довжина l розглянутого ділянки другого проводу. Цей вектор направлений вздовж дроти у напрямку струму. Модуль сили (6.17) буде
Підставивши вираз (6.16) в формулу (6.18), отримаємо такий вираз для сили, з якою перший провід діє на ділянку другого проводу довжини l:
Напрямок сили F21 знайдемо по формулі (6.17). Коли струми I1. I2 течуть в одному напрямку ця сила буде направлена в сторону першого проводу. Сила F12. з якої другий провід діє на ділянку першого проводу довжини l, дорівнює по модулю і протилежна за напрямком силі F21.
Отже, встановлено, що паралельні дроти з струмами, поточними в одному напрямку, притягуються. Неважко довести, що дроти з струмами, поточними в протилежних напрямках, відштовхуються один від одного.
За допомогою формули (6.19) визначена одиниця сили струму в СІ. Як відомо, ця одиниця називається ампер. За визначенням два довгих тонких дроти з струмами силою в один ампер, розташовані парал-лельно на відстані 1 м один від іншого, взаємодіють з силою 2 • 10 -7 Н на 1 м довжини. Підставивши ці значення в формулу (6.19), знайдемо, що магнітна постійна
Одиниця заряду в СІ - кулон - виражається через одиницю сили струму: Кл = А * с. Вимірювання сили взаємодії двох точкових зарядів в 1 Кл привели до значення F = 9 • 10 9 Н при відстані між зарядами R = 1 м. Використовуючи ці значення, знайдемо електричну постійну e0 із закону Кулона
Цікаво відзначити, що величина
чисельно дорівнює швидкості світла в порожнечі.