ланцюгові дроби
Глава I. ПРАВИЛЬНІ КІНЦЕВІ ЛАНЦЮГОВІ ДРОБІ
§1. Подання раціональних чисел ланцюговими дробами
§2. Відповідні дроби. Їх властивості.
Глава II. Нескінченно ЛАНЦЮГОВІ ДРОБІ
§ 1. Подання дійсних ірраціональних чисел правильними нескінченними ланцюговими дробами
1.1. Розкладання дійсного ірраціонального числа в правильну нескінченну ланцюгову дріб.
1.2. Збіжність правильних нескінченних ланцюгових дробів.
1.3. Единственность уявлення дійсного ірраціонального числа правильної нескінченної ланцюгової дробом
§2. Наближення дійсного числа раціональними дробами з заданим обмеженням для знаменника
2.1. Оцінка похибки при заміні дійсного числа його відповідним дробом.
2.2. Наближення дійсного числа відповідними дробами
2.3. Теорема Діріхле.
2.4. Відповідні дроби як найкращі наближення
§3. Квадратичні ірраціональності і періодичні ланцюгові дроби.
§4. Подання дійсних чисел ланцюговими дробами загального виду.
Метою моєї курсової роботи є дослідження теорії ланцюгових дробів. У ній я спробую розкрити властивості відповідних дробів, особливості розкладання дійсних чисел в неправильні дроби, похибки, які виникають в результаті цього розкладання, і застосування теорії ланцюгових дробів для розв'язання низки алгебраїчних задач.
Ланцюгові дроби були введені в 1572 році італійським математиком Бомбелли. Сучасне позначення безперервних дробів зустрічається у італійського математика Катальді в 1613 році. Найбільший математик XVIII століття Леонардо Ейлер перший виклав теорію ланцюгових дробів, поставив питання про їх використання для вирішення диференціальних рівнянь, застосував їх до розкладання функцій, поданням нескінченних творів, дав важливе їх узагальнення.
Роботи Ейлера з теорії ланцюгових дробів були продовжені М. Софронова (1729-1760), академіком В.М. ВисКоватий (1779-1819), Д. Бернуллі (1700-1782) і ін. Багато важливих результати цієї теорії належать французькому математику Лагранжу, який знайшов метод наближеного рішення за допомогою ланцюгових дробів диференціальних рівнянь.
Глава I. Правильні кінцеві ланцюгові дроби.
§1. Подання раціональних чисел ланцюговими дробами.
Ціле число, яке є дільником кожного з цілих чисел
, називається загальним дільником цих чисел. Загальний дільник цих чисел називається їх найбільшим спільним дільником, якщо він ділиться на всякий загальний дільник даних чисел.
- раціональне число, причому b> 0. Застосовуючи до a і b алгоритм Евкліда для визначення їх найбільшого загального дільника, отримуємо кінцеву систему рівностей:
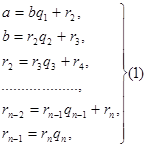
де неповним приватним послідовних поділів
,
, ...,
називаються елементами ланцюгового дробу.
Алгоритм Евкліда дає можливість знайти уявлення (або розкладання) будь-якого раціонального числа у вигляді ланцюгового дробу. Як елементи ланцюгового дробу виходять неповні приватні послідовних поділів в системі рівності (1), тому елементи ланцюгового дробу називаються також неповними приватними. Крім того, рівності системи (2) показують, що процес розкладання в ланцюгову дріб складається в послідовному виділенні цілої частини і перевертанні дробової частини.
Остання точка зору є більш загальною в порівнянні з першою, так як вона може бути застосовна до розкладання в безперервну дріб не тільки раціонального, а й будь-якого дійсного числа.
Розкладання раціонального числа
має, очевидно, кінцеве число елементів, так як алгоритм Евкліда послідовного деленіяa наb є кінцевим.
Зрозуміло, що кожна ланцюгова дріб представляє певне раціональне число, тобто дорівнює певному раціональному числу. Але виникає питання, чи не є чи різні уявлення одного і того ж раціонального числа ланцюгової дробом? Виявляється, що не маються, якщо зажадати, щоб було
.
Теорема. Існує одна і тільки одна кінцева ланцюговий дріб, що дорівнює даному раціональному числу, але за умови, що
.
Доказ: 1) Зауважимо, що при відмові від зазначеного умови єдиність подання відпадає. Справді, при
:
так що уявлення можна подовжити:
наприклад, (2, 3, 1, 4, 2) = (2, 3, 1, 4, 1, 1).
, і так далі; звідси приходимо до наступного висновку про взаємне розташування відповідних дробів:
більше всіх відповідних дробів непарного порядку і менше всіх відповідних дробів парного порядку;
2) відповідні дроби непарного порядку утворюють зростаючу послідовність, а парного порядку - спадну (в разі ірраціонального
зазначені послідовності є нескінченними), тобто
(В разі раціонального
).
-
----
-
---
----
З огляду на те, що при
, переходимо до подальшого висновку, що в разі ірраціонального
,
, ... утворюють стягують послідовність, яка, як відомо, має мати єдину спільну точку, яка є спільним межею послідовностей
,
,
належить всім сегментам послідовності, то
і збігається із зазначеною точкою, так що
.
Отже, ми маємо наступний важливий результат:
нескінченна послідовність відповідних дробів
, яка виникає при розкладанні ірраціонального
, коливаючись близько нього. Або: ірраціональне дійсне
одно межі послідовності відповідних дробів свого розкладання в нескінченну безперервну дріб (процесом виділення цілої частини).
1.2 Відповідність правильних нескінченних ланцюгових дробів.
Тепер покажемо, що сходиться, є послідовність відповідних дробів не тільки такої безкінечної безперервної дробу, яка виникає при розкладанні ірраціонального числа
, але і будь-який нескінченної неперервного дробу
- довільно вибрані цілі позитивні числа.
Але для цього ми заново досліджуємо взаємне розташування відповідних дробів.
З цією метою розглянемо формули:
які справедливі для будь-якої нескінченної неперервного дробу.
1. Формула (1) показує, що будь-яка відповідна дріб парного порядку більше двох сусідніх відповідних дробів, у яких порядок на одиницю менше або більше, ніж у неї, тобто
розташовані зліва від
,
Ця курсова робота показує значення ланцюгових дробів в математиці.
Їх можна успішно застосувати до вирішення невизначених рівнянь виду ax + by = c. Основні труднощі при вирішенні таких рівнянь полягає в тому, щоб знайти якесь його приватне рішення. Так ось, за допомогою ланцюгових дробів можна вказати алгоритм для розвідки такого приватного рішення.
Ланцюгові дроби можна застосувати і до вирішення складніших невизначених рівнянь, наприклад, так званого рівняння Пелля:
(
).
Нескінченні ланцюгові дроби можуть бути використані для вирішення алгебраїчних і трансцендентних рівнянь, для швидкого обчислення значень окремих функцій.
В даний час ланцюгові дроби знаходять все більше застосування в обчислювальній техніці, бо дозволяють будувати ефективні алгоритми для вирішення ряду завдань на ЕОМ.
1. М.Б. Балк, Г.Д. Балк. Математика після уроків. М, «Просвещение», 71.
2. А.А. Бухштаб. Теорія чисел. М, «Просвещение», 96.
3. Алгебра і теорія чисел. Під редакцією Н.Я. Виленкина, М, «Просвещение», 84.
4. І.М. Виноградов. Основи теорії чисел. М, «Наука», 72.
5. А.А. Кочева. Задачник-практикум з алгебри та теорії чисел. М, «Просвещение», 84.
6. Л.Я. Куликов, А.І. Москаленко, А.А. Фомін. Збірник завдань з алгебри і теорії чисел. М, «Просвещение», 93.
7. Е.С. Ляпін, А.Е. Євсєєв. Алгебра і теорія чисел. М, «Просвещение», 74.
8. Математична енциклопедія, том V, М, «Радянська енциклопедія», 85.
9. Ш.Х. Міхеловіч. Теорія чисел. М, «Вища школа», 67.