Калькулятор онлайн - скласти рівняння площини
Цей калькулятор онлайн становить (знаходить) рівняння площини по трьом точкам, лежачим на площині або по нормалі і одній точці лежить на площині.
Онлайн калькулятор для знаходження рівняння площині не просто дає відповідь завдання, він призводить докладний рішення з поясненнями, тобто відображає процес вирішення для того щоб проконтролювати знання з математики та / або алгебрі.
Цей калькулятор онлайн може бути корисний учням старших класів загальноосвітніх шкіл при підготовці до контрольних робіт та іспитів, під час перевірки знань перед ЄДІ, батькам для контролю вирішення багатьох завдань з математики та алгебри. А може бути вам дуже накладно наймати репетитора або купувати нові підручники? Або ви просто хочете якомога швидше зробити домашнє завдання з математики або алгебрі? В цьому випадку ви також можете скористатися нашими програмами з докладним рішенням.
Таким чином ви можете проводити своє власне навчання і / або навчання своїх молодших братів або сестер, при цьому рівень освіти в області вирішуваних завдань підвищується.
Правила введення чисел
Числа можна вводити цілі або дробові.
Причому, дробові числа можна вводити не тільки у вигляді десяткового, а й у вигляді звичайного дробу.
Правила введення десяткових дробів.
У десяткових дробах дрібна частина від цілої може відділятися як точкою так і коми.
Наприклад, можна вводити десяткові дроби так: 2.5 або так 1,3
Правила введення звичайних дробів.
В як чисельник, знаменник і цілої частини дробу може виступати тільки ціле число.
Знаменник не може бути негативним.
При введенні числовий дробу чисельник відділяється від знаменника знаком ділення: /
Введення: -2/3
Результат: \ (- \ frac \)
Ціла частина відділяється від дробу знаком амперсанд:
Введення: -15/7
Результат: \ (-1 \ frac \)
Ці рішення створені і збережені користувачами на нашому сервері
за допомогою цього онлайн-калькулятора.
Загальне рівняння площини
Нехай задані:
прямокутна система координат Oxyz,
довільна площина
крапка
вектор
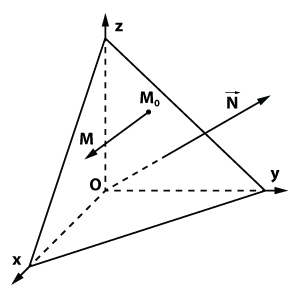
Розглянемо довільну точку М (х; у; z). Точка М лежить на площині тоді і тільки тоді, коли вектори "/> і" /> взаємно перпендикулярні. Так як координати вектора "/> рівні. То в силу умови перпендикулярності двох векторів (скалярний твір має дорівнювати нулю) отримуємо, що точка М (х; у; z) лежить на площині тоді і тільки тоді, коли
Це і є шукане рівняння площині, так як йому задовольняють координати х; у; z будь-якої точки М, що лежить на площині, і не задовольняють координати жодної точки, що не лежить на цій площині.
Розкриваючи дужки, наведемо рівняння (1) до виду
Далі, позначаючи число через, отримуємо
Рівняння (2) називається загальним рівнянням площини. Таким чином, площина є поверхнею першого порядку, так як визначається рівнянням першого ступеня.
Вірно і зворотне: будь-яке рівняння першого ступеня виду (2) визначає в заданій прямокутній системі координат площину. Дійсно, нехай задані прямокутна система координат Oxyz і рівняння з довільними коефіцієнтами А, В, С і D, причому з коефіцієнтів А, В і С хоча б один відмінний від нуля. Дане рівняння свідомо має хоча б одне рішення (якщо, наприклад,, то, взявши довільні х0. І y0. З рівняння отримаємо:).
Таким чином, існує хоча б одна точка M0 (x0; y0; z0), координати якої задовольняють рівняння, тобто Ax0 + By0 + Cz0 + D = 0. Віднімаючи це числове рівність з рівняння Ax + By + Cz + D = 0, отримуємо рівняння
A (x-x0) + B (y-y0) + C (z-z0) + D = 0,
еквівалентну даному. Отримане рівняння (а отже, і рівняння Ax + By + Cz + D = 0) збігається з рівнянням (1) і, отже, визначає площину, що проходить через точку M0 (x0 і перпендикулярну вектору (A; B; C) "/ >.
Вектор (A; B; C) "/>, перпендикулярний площині, називається нормальним вектором або нормаллю цій площині.
теорема
Якщо два рівняння і визначають одну і ту ж площину, то їх коефіцієнти пропорційні, тобто
Кут між двома площинами
Розглянемо дві площини, і, задані відповідно рівняннями
При будь-якому розташуванні площин, і в просторі один з кутів між ними дорівнює куту між їх нормалями (A_1; B_1; C_1) "/> і (A_2; B_2; C_2)" /> і обчислюється за такою формулою:
Другий кут дорівнює
Умова паралельності площин
Якщо площини і паралельні, то колінеарні їх нормалі "/> і" />, і навпаки. Але тоді
"/>
Умова (4) є умовою паралельності площин і
Умова перпендикулярності площин
Якщо площині і взаємно перпендикулярні, то їх нормалі "/> і" /> також перпендикулярні, і навпаки. Тому з формули (3) безпосередньо отримуємо умову перпендикулярності площин і:
Книги (підручники) Книги (інші) Реферати ЄДІ і ОГЕ тести онлайн Ігри, головоломки Побудова графіків функцій Орфографічний словник української мови Словник молодіжного сленгу Каталог школУкаіни Каталог ССУЗовУкаіни Каталог ВУЗовУкаіни Список завдань Знаходження НОД і НОК Спрощення многочлена (множення многочленів) Розподіл многочлена на многочлен стовпчиком обчислення числових дробів Рішення задач на відсотки Комплексні числа: сума, різниця, добуток і частку Системи 2-х лінійних рівнянь з двома змінними Рішення квадрат ого рівняння Виділення квадрата двочлена і розкладання на множники квадратного тричлена Рішення нерівностей Рішення систем нерівностей Побудова графіка квадратичної функції Побудова графіка дрібно-лінійної функції Рішення арифметичної і геометричної прогресій Рішення тригонометричних, показових, логарифмічних рівнянь Обчислення меж, похідної, дотичній Інтеграл, первісна Рішення трикутників Обчислення дій з векторами Обчислення дій з прямими і площинами Площа геометричних ігур Периметр геометричних фігур Обсяг геометричних фігур Площа поверхні геометричних фігур
Конструктор дорожніх ситуацій
Погода - новини - гороскопи
Програми MathSolution.ru на Google Play