ітераційні методи

При великому числі невідомих лінійної системи рівнянь схема методу Гаусса, що дає точне рішення, стає досить складною. В цьому випадку для знаходження коренів зручніше використовувати наближені ітераційні методи. Розглянемо метод ітерацій (метод Зейделя).

Нехай дана система

Припускаючи, що діагональні члени - коефіцієнти системи не дорівнюють нулю

(I = 1, ..., n), дозволимо перше рівняння системи щодо , друге - щодоі т.д. Тоді отримаємо еквівалентну систему:

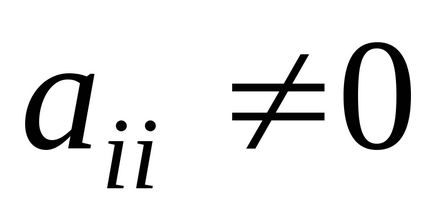
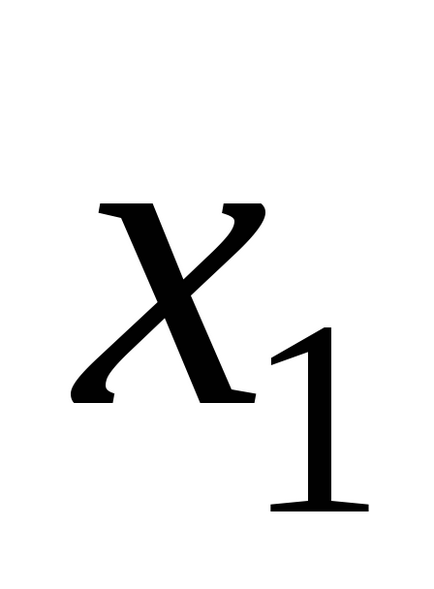
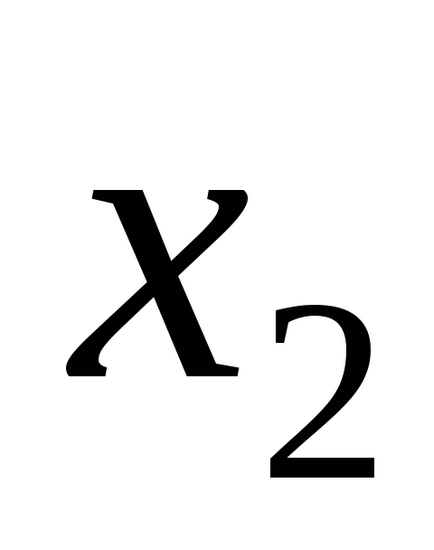
Система (2) вирішується методом послідовних наближень. За нульове наближення можна приймати будь-яке значення. Часто використовують в цій якості стовпець вільних членів.

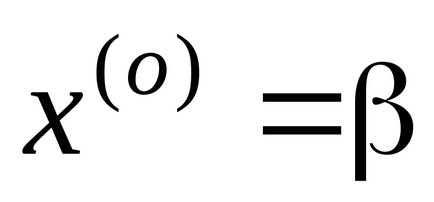
Наступне наближення обчислюють, підставляючи значення

в праву частину рівнянь системи (2). У матричної формі перше наближення виразиться так:

,

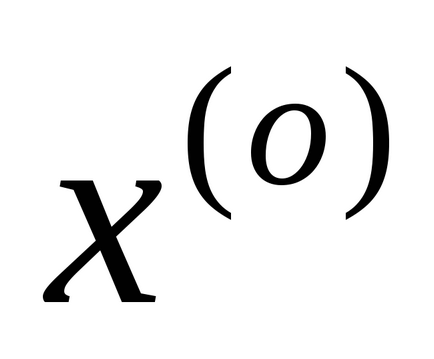
друге наближення обчислюється через перше:

.

Якщо послідовність наближень

має межу

,

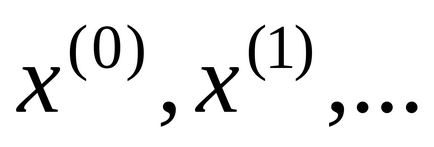
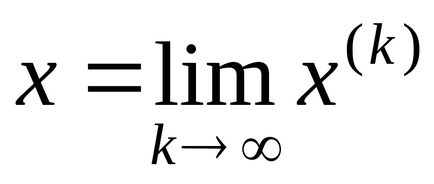
то ця межа є рішенням системи (2), а, отже, і системи (1).

Розпишемо формули наближень в розгорнутому вигляді:

Метод послідовних наближень, який визначається формулою (3), називається методом ітерацій. Ітераційний процес добре сходиться, тобто число наближень, необхідних для отримання коренів системи (1) із заданою точністю, невелика, якщо елементи матриці

малі за абсолютною величиною. Тобто для успішного застосування процесу ітерації модулі діагональних елементів системи (1) повинні бути великі в порівнянні з модулями недіагональних коефіцієнтів цієї системи. Величини вільних членів системи (1) на результат рішення не впливають.

Розглянемо систему лінійних алгебраїчних рівнянь з трьома невідомими:

Виділимо в праву частину з кожного рівняння діагональне невідоме

За нульове (початкова) наближення до вирішення виберемо деякі значення невідомих і позначимо їх

. Підставами початкове наближення в систему (2)

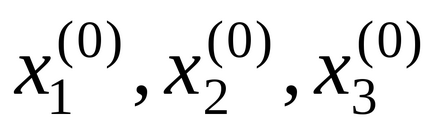
В системі (3) для обчислення невідомих

івикористовувалися тільки що обчислені значення невідомих на поточній ітерації.

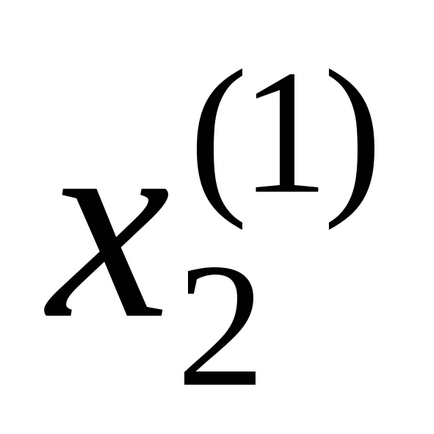
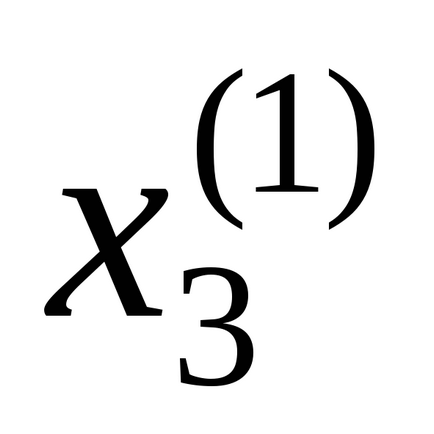
У загальному випадку на k- тієї ітерації система виглядає так:

Тобто, поточне значення невідомих відразу ж використовується для наступних обчислень. Цей метод називається ітераційним методом Гаусса - Зейделя.

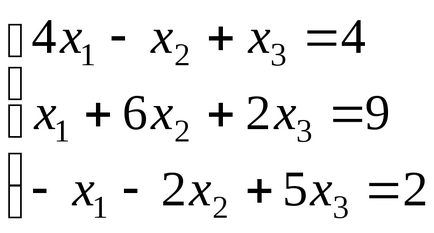
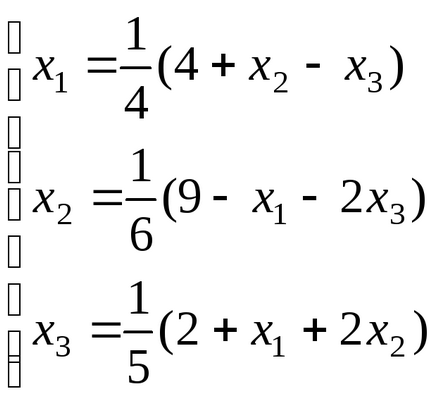
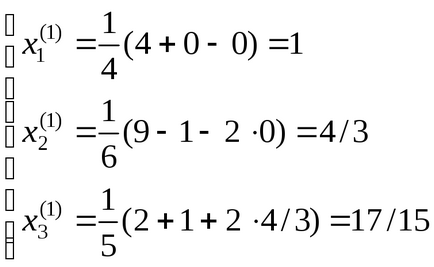
Точне рішення, до якого прагнути ітераційний процес () буде отримано на 5-6-й ітерації.

У разі системи n рівнянь k - е наближення до вирішення матиме вигляд:

Ітераційний процес продовжується до тих пір, поки всі

не стануть близькі. Критерієм близькості може бути умова

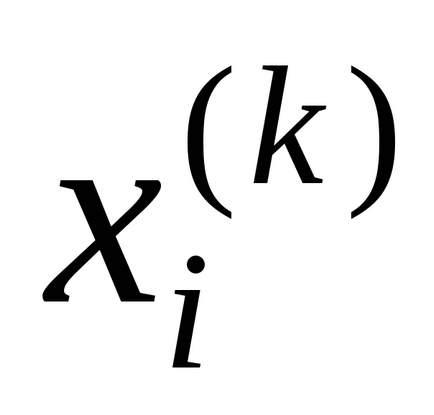
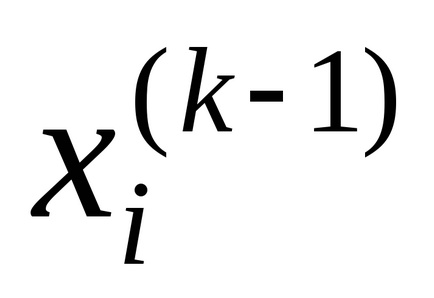
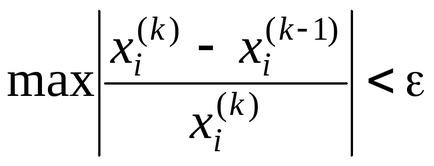
Розглянемо питання збіжності методу. Нехай дана система двох рівнянь

,

З (1) і (3) отримаємо

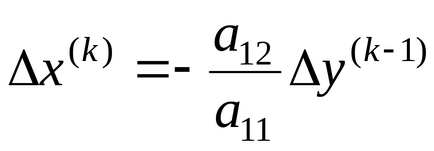
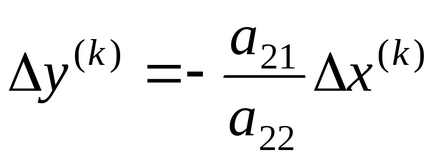
З останніх рівнянь слід:

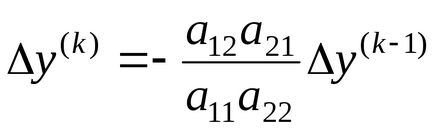
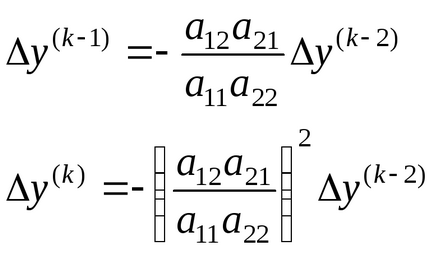
Продовжуючи, можна отримати:

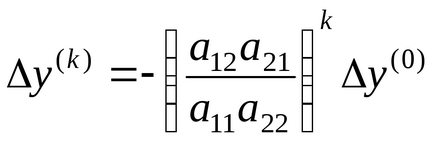
Звідси випливає, що ітераційний процес методу Гаусса - Зейделя

сходиться, якщо наближення на k- ітерації буде істотно відрізнятися від першого наближення. Це можливо тільки при виконанні умови:

,

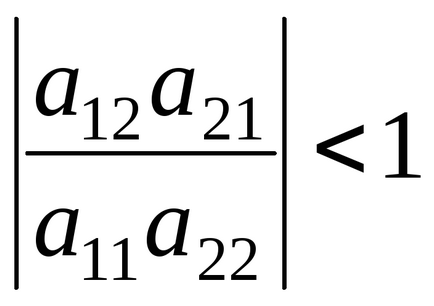
що означає, що діагональні члени превалюють над іншими.

Перевагою метод виключення є те, що він кінцевий і теоретично з його допомогою можна вирішити будь-яку невироджених систему лінійних алгебраїчних рівнянь. Ітераційний метод Гаусса-Зейделя сходиться тільки для спеціальних систем рівнянь. Однак, якщо ітераційний метод сходиться, то він краще:

час обчислень

на одну ітерацію, в той час як для методу виключення час пропорційно, якщо рішення отримано менше, ніж заn ітерацій, то для ітераційного методу загальні витрати будуть менше.

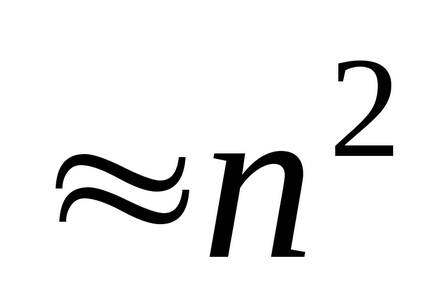
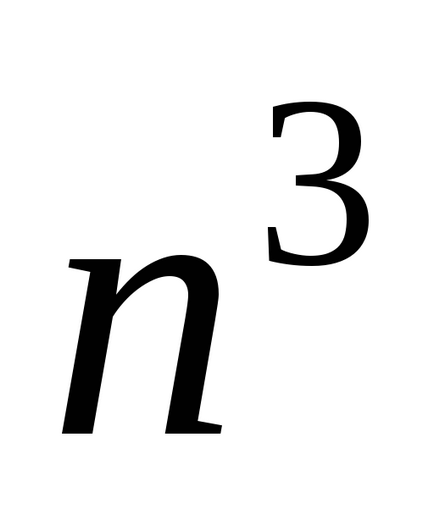
Помилки округлення для ітераційного методу менше.

великі системи рівнянь неможливо точно вирішити за допомогою прямих методів.

Схожі статті

• Як вилікувати енурез у дитини 10 років в домашніх умовах, сайт про методи лікування докторів

• Міжхребцева грижа в попереку, лікування методом терапії та операції

• Метод альпи в плануванні часу