атомна фізика
Сенс квантового числа: воно на одиницю більше числа нулів хвильової функції. значення постійної
визначається з умови нормування.
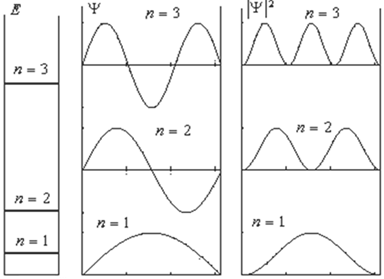
Мал. 4.8. Рівні енергії, хвильові функції і розподіл щільності ймовірностей по координаті x
Відзначимо, що значення, при яких гранична умова в точці також буде виконано, нових станів не дають. Це видно і з виразу для енергії (4.24), в яке n входить в квадраті, і з виразу для хвильової функції (4.25): зміна знака n призведе лише до зміни знака хвильової функції, що залишить незмінним розподіл ймовірностей.
Звідки ж береться дискретність рівнів енергії, характерна і для атома? Порівняємо з вільною часткою: рівняння ті ж, але з іншими граничними умовами! Тут можливі дві постановки задачі. У першому випадку досліджується стан, до якого в класичній механіці відповідало б інфінітное рух (задача розсіювання). Зазвичай в таких випадках рішення можливі при будь-яких значеннях енергії (як кажуть, спектр безперервний). У другому випадку досліджується стан, до якого в класиці відповідає фінітного рух в обмеженій області простору (завдання на зв'язані стани). Вимога кінцівки хвильової функції у всьому просторі веде до квантування енергії. Підкреслимо: у цьому випадку стаціонарне рівняння має фізично прийнятні рішення не завжди, а лише при деяких значеннях енергії. Як наслідок виникає дискретний спектр енергії системи.
Приклад. Визначимо різницю сусідніх рівнів енергії для частинки в нескінченно глибокій потенційній ямі при великих значеннях n. Отриманий результат використовуємо для оцінки різниці енергій сусідніх рівнів енергії поступального руху молекул азоту при кімнатній температурі в посудині. Приймемо масу молекули, а лінійний розмір судини. Порівняємо отриманий результат з кінетичної енергією поступального руху молекул азоту.
Використовуючи вираз (4.24) для рівнів енергії частинки в потенційній ямі, знаходимо різницю енергій сусідніх рівнів
при великих значеннях. Середня кінетична енергія поступального руху молекул азоту дорівнює
Прирівнюючи висловом (4.24) для енергії рівнів частинки в ямі, знаходимо, що така енергія відповідає квантовим числам порядку
Вже сама по собі це число говорить про те, що в області вкрай високих збуджень працюють класичні формули. Різниця енергій сусідніх рівнів виходить, підстановкою в формулу для знайденого виразу для квантового числа:
В електрон-вольтах ті ж характеристики мають значення
Відносна різниця енергій сусідніх рівнів мізерно мала:
і тому в класичному межі квантової дискретністю нехтують.
Частка в тривимірній потенційній ямі
Це узагальнення попереднього завдання. Частка може рухатися в кубічному обсязі з довжиною ребра. Неважко переконатися, що спільне рішення для хвильової функції представимо у вигляді добутку одновимірних хвильових функцій, отриманих в попередньому завданні:
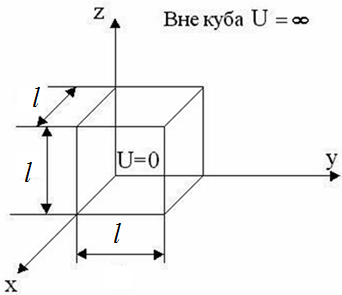
Мал. 4.9. Тривимірна потенційна яма
Стан системи тепер визначається трьома квантовими числами 1. 2 і 3. приймають, як і раніше; цілі значення. Тут ми вперше стикаємося з важливим поняттям виродження енергетичних рівнів, тобто з ситуацією, коли різні стану системи мають однакову енергію. Справді, мінімальна енергія системи досягається при мінімальних значеннях всіх квантових чисел, тобто при 1. 2. 3. Ця енергія дорівнює
і їй відповідає одна хвильова функція. Кажуть, що основне стан не виродилися (невироджені стану з мінімальною енергією - загальне правило). Перше збуджений стан виходить, коли одне з квантових чисел дорівнює 2. а інші як і раніше рівні одиниці; енергія його
Але таку енергію мають тепер три стану з хвильовими функціями,, і (квантове число 2 можна вибрати трьома способами), тому говорять, що кратність виродження першого збудженого рівня дорівнює трьом (g = 3). Природно, в іншій системі може бути зовсім інша кратність виродження (або відсутність такого). Наступні стану частинки в тривимірній потенційній ямі з нескінченними стінками також виродилися. Ясно, що виродження рівнів пов'язане з симетрією системи, з рівноправністю всіх осей. Якби розміри ями були різними 1. 2. 3 то всіма трьома напрямками, то для енергії ми б отримали замість (4.27) вираз
і виродження могло б мати місце лише за певних співвідношеннях між довжиною, шириною і висотою потенційного ящика.
У класичній фізиці пружинний маятник (одновимірний осцилятор) являє собою точкове тіло масою m, прикріплене до пружини і нестійке з круговою частотою. Потенційна енергія такої системи описується виразом
так що рівняння Шредінгера записується у вигляді
Звідси можна знайти рішення для хвильової функції основного стану
Підставляючи цей вираз в рівняння Шредінгера, легко переконатися, що енергія основного стану дорівнює
Ми не виписуємо хвильові функції збуджених станів осцилятора, але вираз для дозволених значень енергії має вигляд (- коливальний квантове число)