4 Нечіткі числа
4.1 Поняття нечіткого числа
Нечіткі числа - це нечіткі змінні на числової осі, іншими словами, нечітке число визначається як нечітка множина

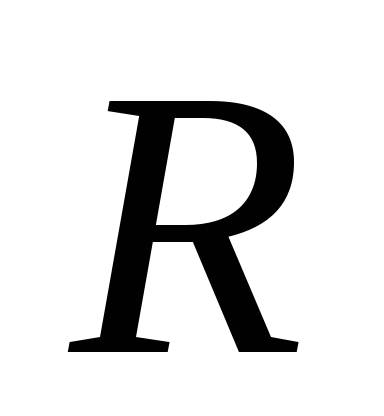
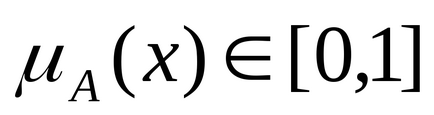
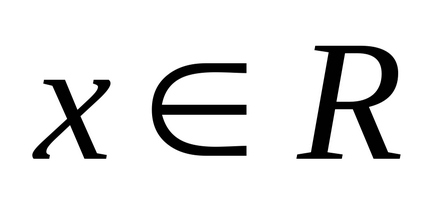
Нечітке число називається нормальним. якщо і опуклим. якщо для будь-яких
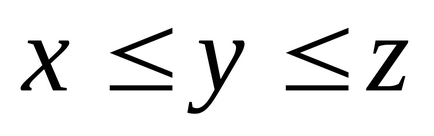
.
безліч


.
підмножина
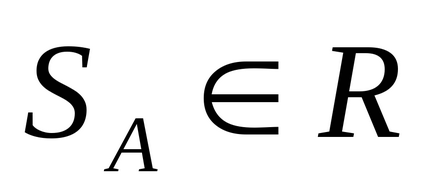

.
Нечітке число унімодальне. якщо умова
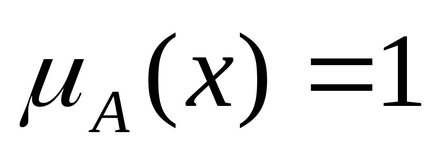
Опукле нечітке число називається нечітким нулем, якщо
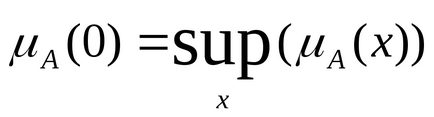
Нечітке число позитивно. якщо

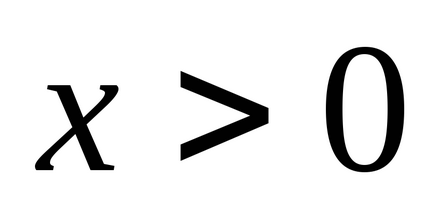

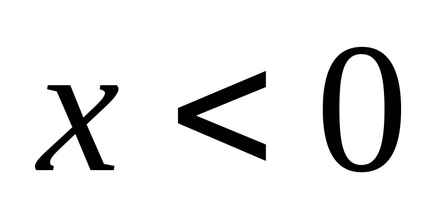
4.2 Операції над нечіткими числами
Розширені бінарні арифметичні операції (додавання, множення та ін.) Для нечітких чисел визначаються через відповідні операції для чітких чисел з використанням принципу узагальнення наступним чином:
Використовувати певні таким чином алгебраїчні операції над нечіткими числами недоцільно, зважаючи на великий обсяг обчислень. Тому часто використовують уявлення нечітких чисел в
Нечітке число в
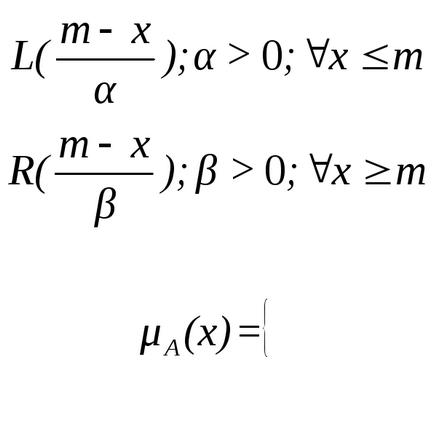
де
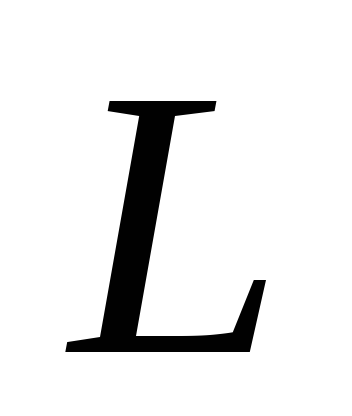
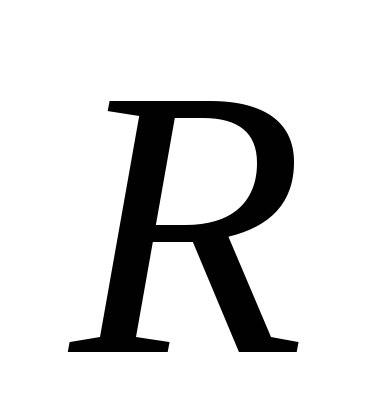
,
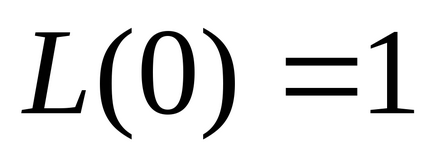
функція
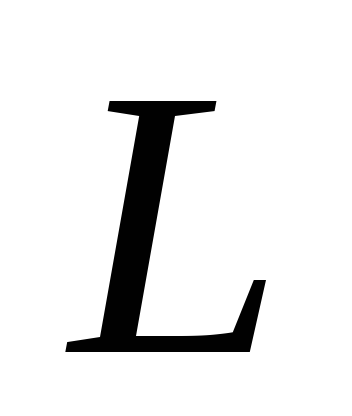
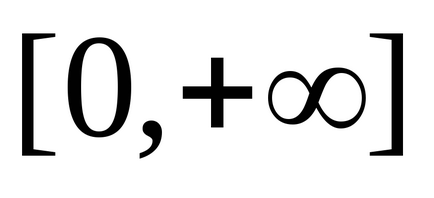
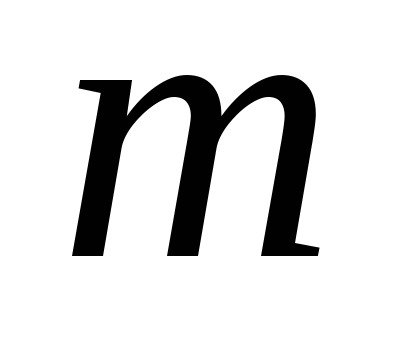





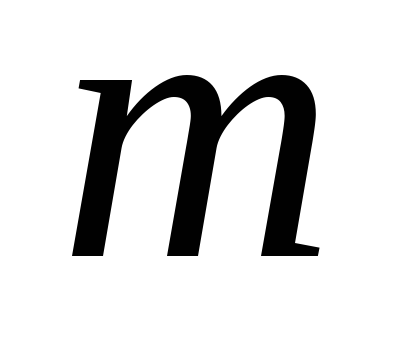
Таким чином, нечітке число в
На практиці

Крім того, набули поширення трапецієподібні форми функцій належності, які мають вигляд
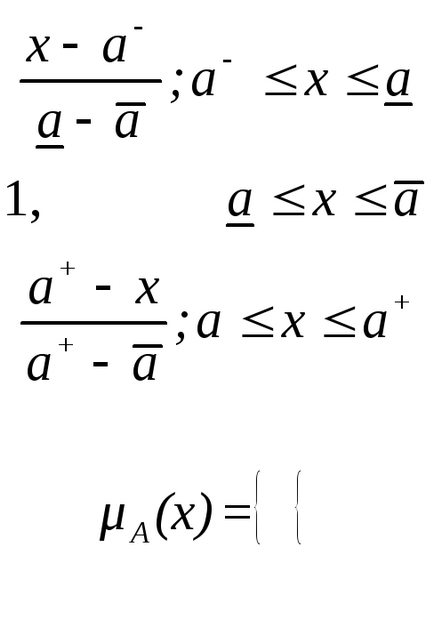
Рішення задач математичного моделювання складних систем із застосуванням апарату нечітких множин вимагає виконання великого обсягу операцій над різного роду лінгвістичними та іншими нечіткими змінними. Для зручності виконання операцій, а також для введення-виведення і зберігання даних, бажано працювати з функціями приналежності стандартного типу.
На жаль, навіть при зведенні нечітких чисел до поняття трикутних чисел, залишаються невирішеними проблеми протилежної і зворотного елементів і властивість дистрибутивности. Ще один істотний недолік такого підходу. Розмитість твори залежить не тільки від розмитості сомножителей, але і від того, яке місце дані нечіткі числа займають на числової осі. Наприклад, нехай
А = (1, 2, 3), В = (2, 3, 4), тоді АВ = (2, 6, 12)
і С = (99, 100, 101), Е = (100, 101, 102),
тоді РЄ = (9 900, 10 100, 10 302).
З цього прикладу випливає, що РЄ більш розмито, ніж АВ.
Нечіткі множини, які доводиться застосовувати в більшості завдань, є, як правило, унімодальне і нормальними. Одним з можливих методів апроксимації унімодальних нечітких множин є апроксимація за допомогою