Ноу Інти, лекція, нечіткі числа і операції над ними
Анотація: В лекції дається визначення нечіткого числа, розглядаються його властивості, описуються операції над нечіткими числами. Докладно розглядаються нечіткі трикутні числа, а також різні арифметики нечітких трикутних чисел.
Основні визначення
Нечітке число - це нечітке підмножина універсальної множини дійсних чисел, що має нормальну і опуклу функцію приналежності, тобто таку, що: а) існує значення носія, в якому функція приналежності дорівнює одиниці, а також b) при відступі від свого максимуму вліво або вправо функція власності не зростає.
Нечітке число унімодальне. якщо умова справедливо тільки для однієї точки дійсної осі.
Опукле нечітке число називається нечітким нулем. якщо
Підмножина називається носієм нечіткого числа, якщо
Нечітке число позитивно. якщо, і негативно. якщо.
Відповідно до принципу узагальнення Заде було введено поняття арифметичних операцій на безлічі нечітких чисел. Для довільних нечітких чисел і для будь-яких чисел справедливо
Розширені бінарні арифметичні операції (додавання. Множення та ін.) Для нечітких чисел визначаються через відповідні операції для чітких чисел з використанням принципу узагальнення наступним чином:
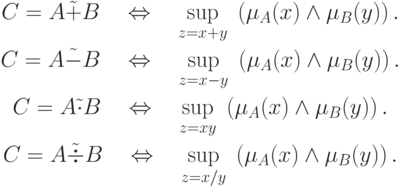
Аналіз властивостей арифметичних операцій над нечіткими числами показав, що нечітке число не має протилежного і зворотного чисел, додавання і множення комутативні, асоціативні і в загальному випадку недістрібутівни.
При вирішенні задач математичного моделювання нечітких систем можна використовувати нечіткі числа (L-R)-типу. які передбачають більш просту інтерпретацію розширених бінарних відносин.