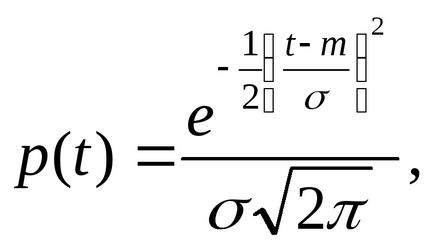3 Постановка завдання
4 Вхідна і вихідна інформація
До вхідних даних відноситься:
а) інтервал часу, через який приходять дзвінки абоненту;
б) інтервал часу, який з'єднані абоненти використовують для передачі інформації;
в) стан мобільного рахунку абонента (НЕ залишкового);
г) ймовірність здійснення дзвінка, і його ймовірність на з'єднання.
До вихідних даних слід віднести інформацію, виведену в процесі функціонування процесу моделювання:
а) кількість обслужених абонентів мобільного мережею;
б) загальна сума хвилин, використана абонентом, так і абонентами разом;
в) кількість успішних з'єднань.
г) прибуток мобільних операторів в загальному.
5 Математичний опис задачі
Система може бути представлена у вигляді схеми масового обслуговування. Дамо опис диною схеми.
Завдання масового обслуговування виникають в тих випадках, коли умови на виконання роботи надходять у випадкові моменти часу, а виконання цих робіт і виробляються одним або декількома обслуговуючими пристроями. Тривалість обслуговування окремих заявок є випадковою.
Пристрій, здатний в будь-який момент часу обслуговувати лише одну заявку, називається каналом обслуговування. Характерною особливістю завдань масового обслуговування є виникнення невідповідності між швидкістю надходження заявок і швидкістю обслуговування, внаслідок чого або виявляються такими, що простоюють обслужених прилади, або утворюється черга на обслуговування. Тому принциповий інтерес представляють наступні характеристики СМО:
довжина черги в різні моменти часу;
загальна тривалість перебування заявки в системі обслуговування;
приватна часу, протягом якого обслуговують прилади не були зайняті.
Для отримання математичної моделі СМО необхідно мати:
опис вхідного потоку заявок;
опис способу, яким виконується обслуговування;
опис дисципліни черги, тобто вказівка того, чином заявки надходять з черги на обслуговування.
Одним з основних підходів, які використовуються при побудові математичних моделей процесів функціонування систем, є Безперервна-стохастичний підхід. Особливості цього підходу виражаються у використанні як типових математичних схем систем масового обслуговування (англ. Queuing system).
Схеми масового обслуговування є класом математичних схем, розроблених в теорії масового обслуговування і різних застосуваннях для формалізації процесів функціонування систем, які по суті своїй є процесами обслуговування.
Процес обслуговування може бути різним по своїй фізичній природі: процеси функціонування економічних, виробничих, технічних та ін. Систем, наприклад: потоки поставок продукції деякого підприємству, потоки деталей і комплектуючих виробів на складальному конвеєрі цеху, заявки на обробку інформації ЕОМ від віддалених терміналів і т . Д.
При цьому характерною для роботи таких об'єктів є випадкове поява заявок на обслуговування і завершення обслуговування в випадкові моменти часу, тобто стохастичний характер процесу їх функціонування.
У будь-якому елементарному акті обслуговування можна виділити дві основні складові: очікування обслуговування заявкою і власне обслуговування заявки. Це можна зобразити у вигляді деякого


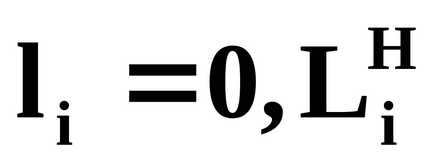




Рис.5.1. Прилад обслуговування заявок.
Потоком подій називається послідовність подій, які відбуваються одна за одною до деяких випадкові моменти часу.
Зазвичай при моделюванні різних систем щодо елементарного каналу обслуговування

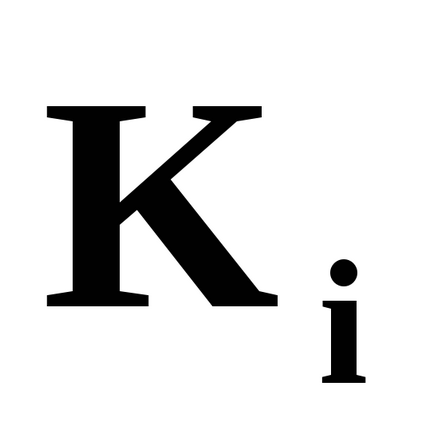

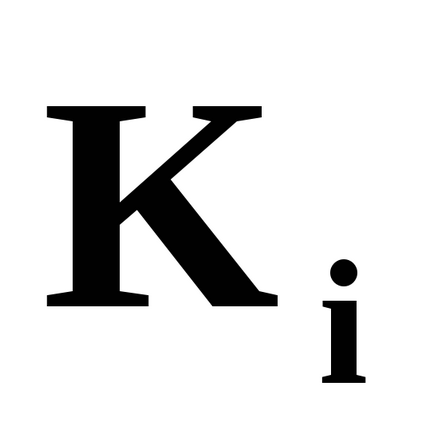
У даній роботі розглядається випадок одного каналу, на який надходить потік вимог з інтенсивністю

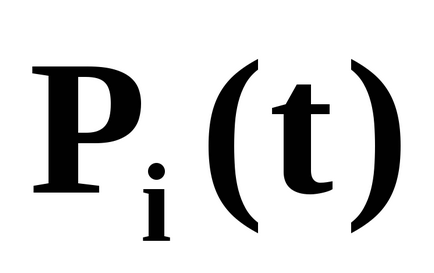


значення

і має сенс тільки при
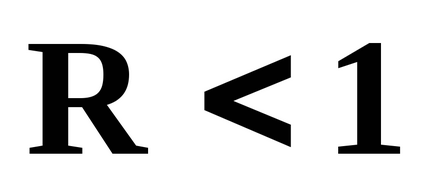
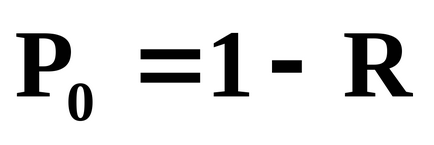
З урахуванням цього виразу

Основними характеристиками в системі є середня довжина черги і середній час очікування обслуговування.
Середнє число заявок, які знаходяться в системі обслуговування
.
Можна також знайти середнє число заявок
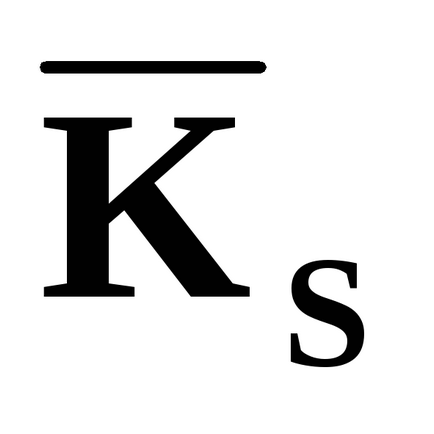
різниця між

З огляду на середній час обслуговування однієї заявки отримуємо вираз:
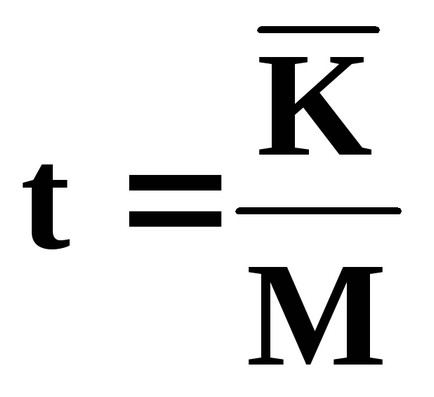
Система «Зупинка маршрутного таксі» являє собою типову систему масового обслуговування. Каналами обслуговування є маршрутні таксі, які чекають наповнення, транзактами - пасажири і таксі, яке прибувало на зупинку. Приватність каналу відповідає наявності порожній маршрутки на кінцевій зупинці. Схема даної системи одноканальна і однофазна, оскільки існує тільки один маршрут і щоб дістатися міста не треба пересідати на інший вид транспорту. Періоди приходу пасажирів і прибуття маршрутних таксі підкорюють нормальному закону розподілу з математичними очікуваннями біля 8.00 і 17.00 і дисперсією приблизно в 1 ч.
Даний закон розподілу виражається формулою: