Зна плоскої кривої
Розглянемо довільну безперервну криву АВ. яка не має точок самопересеченія. Якщо в кожній її точці М провести дотичну, то вона при переміщенні Т.М від А до В буде повертатися.
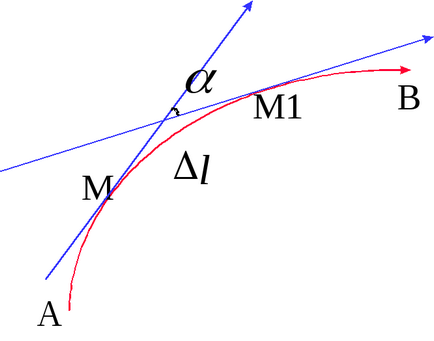
Цим крива відрізняється від прямої, де дотична завжди спрямована однаково, а саме: зливається з прямою.
Чим швидше повертається дотична, тим більше викривлена крива лінія, тим більше її "кривизна".
Дамо математичне визначення кривизни кривої. Розглянемо довільну дугу ММ1, в точках М і М1 проведемо дотичні. Нехай кут між ними , він назив кутом суміжності, дугаММ1 = S. Тоді відношення / S звані. середньої кривизною кривої АВ на ділянці ММ1. Середня кривизна показує величину кута повороту дотичній при переміщенні точки М на одиницю довжини по кривій. На різних ділянках кривої середня кривизна змінюється. Лише для однієї кривої - кола середня кривизна постійна: КСР = / S = / (R) = 1 / R, ті для окружності кривизна є величина зворотна радіусу.
Для точної характеристики викривленості кривої вводять поняття кривизни в точці, позначають К.
Кривизною кривої в Т.М звані межа (якщо він сещ-ет), до якого прагне середовищ кривизна дуги ММ1, коли т.М1 по кривій прагне до М.
К = limS

Межа (1) є не що інше як похідна кута нахилу дотичній по довжині дуги, а тому остання межа є границя відношення приросту функції до пріращена аргументу, тобто похідна: К = d / dS, (2).
Таким чином, кривизна кривої в точці є похідна кута нахилу дотичній по довжині дуги кривої. Кривизна є число невід'ємне, тому насправді К = | d / dS |, (2 ').
З ф-ли (2) кривизни отримаємо зручну на практиці ф-лу, коли крива задається параметрично.
Припускаємо додатково, що функції (t), (t) мають безперервні похідні 1 та 2 порядків і xt '= ' (t) при t відповідному Т.М.
Тоді dS =, определімd.
d =, підставляючи dS, d в (2 ') отримаємо К = |
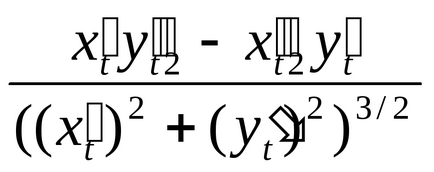
Якщо крива задана явним рівнянням у = f (х) вважаємо параметр t = х, тоді
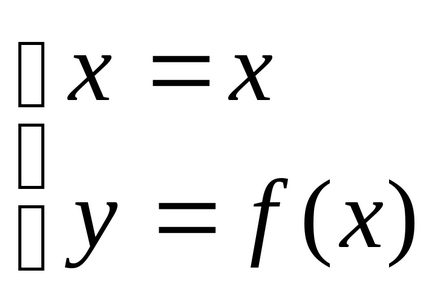
Якщо крива задана полярним рівнянням , то вважаючи t = отримаємо
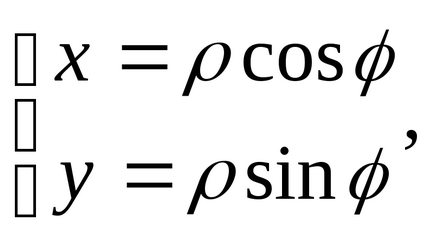
Приклад. Визначити кривизну кривої у = sinх в Т.Х = П / 2 -самостійне.
§3.Радіус, коло і центр кривизни. Поняття еволюти і евольвенти.
Визначення: величина R, зворотна кривизні кривої К в точці, звані радіусом кривизни кривої в цій точці: R = 1 / К. Для прямої радіус кривизни дорівнює бескон-ти, ті пряма це коло нескінченного радіуса.
Для окружності Радус крівізни- це її звичайний радіус, для кривих, заданих в параметричній формі або явними рівняннями у = f (х) або радіус кривизни знаходиться за формулами легко одержуваних з (3) - (5). Так для у = f (х) R = 1 / К =, і т.п. (самим).
Побудуємо в Т.М кривої нормаль до неї і відкладемо в сторону угнутості відрізок МС = R.
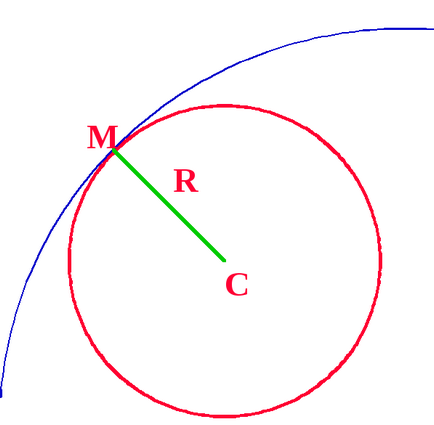
Точка С звані центром кривизни в даній Т.М, коло (коло) з центром С і радіусом R звані кругом (колом) кривизни лінії в Т.М. У Т.М крива і окружність кривизни їм однакову кривизну К, тому дугу кривої поблизу М з малою помилкою можна замінювати дугою кола кривизни в цій точці.
Кожній точці М кривої (L) відповідає своя точка С- центр кривизни в Т.М.
Геометричне місце центрів кривизни кривої (L) називається її еволюта (L '). (L ') - є теж певна крива. По відношенню до (L ') вихідна крива (L) називається евольвентою або рядків. Існують формули. що дозволяють з даного рівняння кривої (L) написати рівняння еволюти. І навпаки.
Практично еволюта по даній кривій можна побудувати так. Можна довести, що кожна нормаль до кривої (L) явл. дотичній до еволюта. Тому побудувавши достатню кількість нормалей проводимо до них криву, яка стосується всіх цих нормалей- огибающую сімейства нормалей.
Евольвенту по еволюта можна побудувати механічним способом.
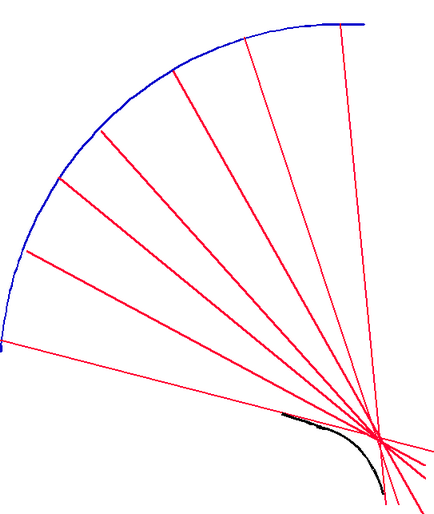
Нехай гнучка лінійка зігнута по виду еволюти С0 С. Прикріпимо до кінця С0 нитку і туго натягнемо на лінійку.
Якщо тепер цю нитку розгортати, натягуючи її весь час за вільний кінець, то він опише криву, яка буде евольвентою кривої С0 С. Оскільки нитки можуть мати різну довжину, то евольвент у одній еволюти може бути скільки завгодно.