зіткнення тел
Існують два граничних випадки удару: абсолютно пружний і абсолютно непружних. Абсолютно пружним називається удар, при якому механічна енергія тіл не переходить в інші види енергії. При такому ударі кінетична енергія переходить повністю або частково в потенційну енергію пружної деформації. Потім тіла повертаються до початкової формі, відштовхуючи один одного, і потенційна енергія знову переходить в кінетичну, і тіла розлітаються зі швидкостями, обумовленими за законами збереження енергії та імпульсу.
Абсолютно непружних удар характеризується тим, що потенційної енергії деформації не виникає. Кінетична енергія тел повністю або частково переходить у внутрішню енергію. Після удару зіткнулися тіла або рухаються разом, або спочивають. При такому ударі виконується закон збереження імпульсу, закон же збереження механічної енергії не виконується.
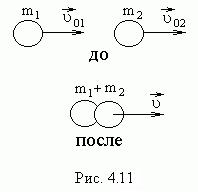
Розглянемо абсолютно непружних удар двох частинок (матеріальних точок), що утворюють замкнену систему (рис. 4.11). Маси часток і. їх швидкості до удару і. Після удару швидкості частинок однакові і рівні. Згідно із законом збереження імпульсу маємо:
Тоді швидкість частинок після удару.
Тепер розглянемо абсолютно пружний удар, обмежившись розглядом центрального удару двох однорідних куль. Удар називається центральним, якщо до удару кулі рухаються вздовж прямої, що проходить через їх центри. При центральному ударі зіткнення може статися, якщо кулі рухаються назустріч один одному (рис. 4.12), або один з куль наздоганяє інший (рис.4.13).
Будемо припускати, що кулі утворюють замкнену систему і обертання куль відсутня.
Маси куль і. їх швидкості до удару і. Після удару їх швидкості і. Згідно із законом збереження енергії
Помноживши рівняння (4.15) на 2 і згрупувавши, отримуємо:. або З (4.16)
Розділимо перше з цих рівнянь на друге
Помножимо (4.18) на і віднімемо результат з (4.17)
З виразів (4.19) видно, що після удару швидкості куль не можуть бути однаковими. Дійсно, якщо прирівняти і. отримуємо =. тобто швидкості куль повинні бути однаковими і до удару, але в цьому випадку зіткнення не може відбутися.
Розглянемо випадок, коли маси соударяющихся куль рівні. При цьому, як випливає з (4.19) і. тобто кулі при зіткненні обмінюються швидкостями.
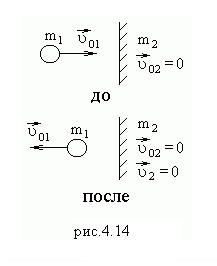
При розгляді абсолютно пружного удару кулі про нерухому або рухому стінку останню слід розглядати як куля нескінченно великої маси. Тоді розділивши чисельник і знаменник виразу (4.19) на (масу стінки) і вважаючи 0, отримаємо.
Якщо стінка нерухома (ріс.4.14), = 0, швидкість кулі змінює свій напрямок на протилежне, модуль швидкості залишається незмінним.