Завдання на кмітливість, сайт домашнє завдання
У цьому розділі представлені завдання, для вирішення яких треба мати не тільки нестандартне мислення, кмітливість і логіку, а й гарна просторова уява. Адже при вирішенні геометричних задач ми стикаємося з розташуванням предметів у площині і просторі, нам треба добре уявляти розміри речей і відстань між ними.
Спробуйте спочатку вирішити задачу в розумі, не вдаючись до допомоги підручних предметів. Закрийте очі, уявіть собі всі речі, які описані в завданні, спробуйте подумки покриття їх, оглянути з різних сторін. Уявіть все - колір, матеріал, спробуйте відчути їх вагу. Отримайте задоволення від володіння цією річчю, адже головне в наших завданнях - це радість, яке ви від них отримуєте.
Все це допоможе вам у вирішенні, поліпшить просторове мислення, дасть можливість з легкістю вирішити математичні умови задач. Перші завдання, можливо, будуть даватися з великими труднощами, але чим більше ви їх вирішите, тим простіше вони будуть здаватися, і частіше буде приходити в голову вже готове рішення вже при читанні завдання.
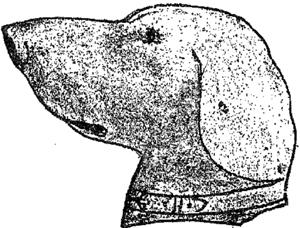
Маша отримала в подарунок пряник у вигляді собачої голови та вирішила розділить його порівну зі своїм молодшим братом. Бажаючи бути справедливою, вона хотіла б знати, яким чином це зробити, щоб обидві частини були однакових розмірів і форми.
Чи не зумієте ви правильно намалювати ці доріжки?
сварливі сусіди
Розповідають, що три сусіда, які володіли спільно невеликим парком, який ви бачите на малюнку, один раз пересварилися між собою. Власник великого будинку, скаржачись, що його турбують сусідські кури, проклав обгороджену доріжку від своїх дверей до хвіртки внизу малюнка. Тоді людина, що живе в правому будиночку, проклав доріжку до лівої хвіртки, а людина з лівого будиночка проклав доріжку до хвіртки справа. Жодна з доріжок не перетинаються з іншими.
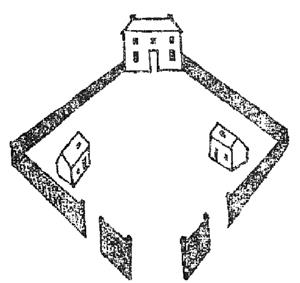
Чи не зумієте ви правильно намалювати ці доріжки?
Юні теслі

Картинка говорить сама за себе, і не треба бути Шерлоком Холмсом, щоб зрозуміти, що хлопці знайшли на горищі старий ящик з інструментом а їх мати пішла у своїх справах. Важче уявити собі як Жучка зможе вибратися з будки через маленькі дверцята, коли хлопці приколоти до будці останню стінку. Однак надамо Жучку самої себе і не будемо витрачати часу на несуттєві для нас побутові подробиці.
Як найкраще розрізати на мінімальне число частин квадратну кришку кухонного столу, щоб з них можна було сколтов відсутню стінку буди?
завдання столляра

Ті, хто вивчає геометрію, знайдуть тут цікаву елементарну задачу, яку найкраще вирішувати експериментальним шляхом, хоча правильна відповідь можна знайти і теоретично, користуючись якимось прийомом, що вельми нагадує знаменитій Сьомій пропозицію Евкліда.
У столяра була дошка довжиною в 4 і шириною в 2 фути зі зрізаним кутом. Цю дошку потрібно розрізати на мінімальне число частин без всяких відходів так, щоб з них можна було скласти правильну квадратну кришку столу, показаного на малюнку.
В даному конкретному випадку відсутній шматок дошки зрізаний під кутом 15 градусів, але коли ви вирішите головоломку, то виявите, що спосіб її вирішення годиться як у випадку більшої, так і менші за розміром кута.
Розріжте дошку на мінімальне число частин, з яких можна було б скласти правильний квадрат?
Скільки виноградних лоз можна посадити на квадратному ділянці в 1/16 акра так, щоб відстояли один від одного не менше ніж на 9 футів?
ПРИМІТКА: Це завдання зручно підібрана, щоб випробувати винахідливість наших математиків, нагадаємо лише, що у квадрата площею в 1 акр сторона дорівнює 208 і 710/1000 фути, а значить, сторона квадрата площею в 1/16 акра становить 52 фути 2 дюйма ( тут дається округлене значення. В одному футі міститься 12 дюймів). Це дещо відрізняється від прийнятих в сільській місцевості вимірювань, де квадрат зі стороною в 210 футів вважається рівним 1 акру.
Нова зірка
Ця незвичайна головоломка пов'язана з недавньою заявою одного астронома про те, що він виявив нову зірку першої величини.
На наведеному тут малюнку Ви бачите цього високовченого професора, що знайомить зі своїм відкриттям побратимів-астрономів. Він уже зобразив на дошці як зображені п'ятнадцять зірок різної величини, і тепер збирається показати, де саме знаходиться відкрита ним нова зірка.
Чи зумієте Ви намалювати п'ятикутну зірку, яка була б більше за інші із зображених на малюнку зірок і не перетиналася б при цьому ні з однією з них!

Куди можна помістити ще одну зірку першої величини?