Завдання еліпсоїд обертання
Завдання. За двома параметрами еліпсоїдів, наведених в Додатку, обчислити інші головні параметри і порівняти їх з параметрами еліпсоїда WGS 84. Схематично показати окремі елементи на кресленні.
Еліпсоїд обертання, його елементи і співвідношення між ними.
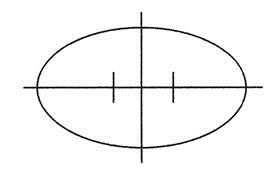
Де - велика, або екваторіальна піввісь еліпсоїда, - мала або полярна піввісь (Рис.1).
Перетину поверхні еліпсоїда площинами, перпендикулярними осі обертання, є окружність, звані паралелями. Найбільша паралель, площина якої проходить через центр еліпсоїда О, називається екватором. Екватор ділить еліпсоїд на дві однакові половини: південну і північну.
Площині, що проходять через малу вісь еліпсоїда, називаються меридіанними площинами, а перетину ними поверхні еліпсоїда - меридіанами.
Меридіанні перетину є еліпси. відстань від
Центру еліпса до кожного з фокусів, рівне, називається лінійним ексцентриситетом, а відношення лінійного ексцентриситету до великої або малої півосі - ексцентриситетом еліпса. Відповідно до цього розрізняють перший і другий ексцентриситет меридіанного еліпса:
Перший ексцентриситет - (2)
Другий ексцентриситет - (3)
Лінійні елементи - велика і мала півосі - визначають розміри еліпсоїда, а ексцентриситет - його форму, іншими словами, велику або меншу приплюснути біля полюсів. Чим більше різниця між великою і малою півосями, тим більше ексцентриситет, і навпаки. У сфери він дорівнює нулю.
Форму еліпса визначає також інша відносна величина, так зване полярне стиснення, або просто стиснення еліпсоїда, що обчислюється за формулою: (4)
Як випливає з формули (1), еліпсоїд обертання повністю визначається двома елементами - великої і малої півосями. Замість малої півосі часто використовують стиснення або ексцентриситет. Один з двох заданих елементів обов'язково повинен бити лінійним.
Разом з співвідношеннями (2) - (4) між елементами еліпсоїда існують наступні залежності:
Вони випливають безпосередньо з формул (2) і (3). Якщо покласти:
Шляхом нескладних перетворень можна отримати:
Полярний радіус кривизни (його іноді називають головним) дорівнює:
. Основними радіусами кривизни в деякій точці, є:
М - в площині меридіана,
N - в площині першого вертикалі (перший вертикал, - площина, що проходить через нормаль до еліпсоїда ортогонально до площини меридіана),
- середній радіус кривизни. На екваторі радіус кривизни меридіана (М) мінімальний, екватора (N) і середній радіус кривизни (R) визначаються виразами:
З формул (4) і (7), що, звідки.
Для земного еліпсоїда, при оріентірних обчисленнях, можна прийняти:.
Значення і в сферичної геодезії визначають величини першого порядку малості, і - другого порядку малості, і так далі.
Завдання Еліпсоїд обертання - 4.5 out of 5 based on 2 votes