закони Кірхгофа
,
.
Перший закон Кірхгофа часто називають законом Кірхгофа для струмів і скорочено в тексті позначають ЗКТ.
Число незалежних рівнянь дорівнює трьом, так як будь-яка з цих рівнянь відрізняється від суми трьох інших тільки знаком. Отже, якщо ланцюг містить
вузлів, то для неї можна скласти за першим законом Кірхгофа
незалежних рівнянь. Сукупність з N вузлів ланцюга, рівняння для яких утворюють систему лінійно незалежних рівнянь, називають сукупністю незалежних вузлів ланцюга.
Приклади на застосування першого закону Кірхгофа. Паралельне з'єднання елементів
Як приклад на застосування першого закону Кірхгофа розглянемо паралельне з'єднання декількох елементів активних опорів, конденсаторів, котушок індуктивності.
Особливістю паралельного з'єднання декількох елементів є рівність напруг, прикладених до затискачів будь-якого з елементів, що входять в з'єднання. Ланцюг при такому з'єднанні характеризується тільки одним незалежним вузлом.
Нехай паралельно з'єднані n елементів активного опору. Якщо вибрати напрямки звітів струмів в елементах такими як це показано на малюнку 3, то згідно з першим законом Кірхгофа при паралельному з'єднанні елементів запишемо:
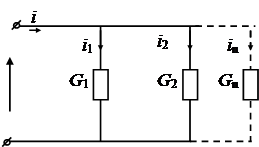
,
.
не відрізняється від залежності між напругою на затискачах і струмом в елементі активного опору з провідністю G. Отже, ланцюг, складена з декількох опорі, включених паралельно, може бути замінена одним активним опором, при цьому провідність еквівалентного елемента дорівнює сумі провідностей елементів, що входять в з'єднання .
При паралельному з'єднанні конденсаторів (малюнок 4) струм гілки можна визначити за формулою:
.
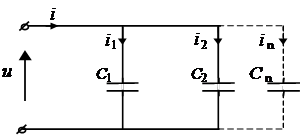
Для обчислення загального струму необхідно підсумувати струми гілок:
,
. .
Таким чином, при паралельному з'єднанні декількох конденсаторів еквівалентна ємність дорівнює сумі ємностей, що входять в з'єднання.
У разі паралельного з'єднання котушок індуктивностей (рисунок 5)

ток кожної з гілок дорівнює:
.
Рівняння для обчислення загального струму має вигляд:
.
.
Це означає, що значення еквівалентної індуктивності будить менше найменшого із значень з'єднаних паралельно индуктивностей.
Другий закон Кірхгофа
Другий закон Кірхгофа формулюється так: алгебраїчна сума напруг гілок в будь-якому контурі ланцюга тотожно дорівнює нулю. Для замкнутого контуру, зображеного на малюнку 6, можна записати співвідношення:
.
Для визначення всіх струмів і напруг в схемі досить знайти значення струмів у всіх гілках ланцюга. Знаючи струм, що проходить через будь-яку з гілок ланцюга, можна знайти як напруга цієї гілки, так і напругу між будь-якою парою вузлів ланцюга.
Якщо ми поставимо собі довільно позитивними напрямками струмів в гілках ланцюга і пронумеруємо довільно ці струми, то за першим законом Кірхгофа можна скласти
рівнянь щодо струмів в гілках ланцюга.
За другим законом Кірхгофа буде
лінійно-незалежних рівнянь для напружень
рівнянь за першим законом Кірхгофа, і
рівнянь, складених за другим законом Кірхгофа, утворює систему
лінійно - незалежних рівнянь. Ця система буде неоднорідною системою рівнянь, так як її вільними членами є задані напруги джерел.
Подібна система рівнянь має єдине рішення, що дозволяє знайти струми в гілках ланцюга, а по ним і значення напруг між будь-якою парою вузлів ланцюга.
Для прикладу складемо систему рівнянь за першим законом Кірхгофа (рисунок 10).
.
,
,
.
У той же час за другим законом Кірхгофа для контурів I, II, III можна скласти систему з
.
,
,
.
Таким чином, вирішуючи систему з 6 рівнянь з шістьма невідомими струмами, наприклад за методом Крамера, визначимо невідомі. Якщо в ланцюзі буде джерело струму, то в системі рівнянь невідомим буде напруга на затискачах цього джерела, а струм через джерело буде дорівнює струму задає джерела. Загальна кількість невідомих збережеться колишнім.
Для ланцюга (малюнок 11) визначити струми
, якщо E = 20 В, I0 = 2 A, R1 = 15 Ом, R2 = 85 Ом.
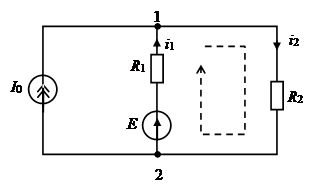
Виберемо напрямки струмів
,
і обходу в контурі, складемо рівняння за законами Кірхгофа. Число рівнянь, що складаються за першим законом Кірхгофа:
.
Число рівнянь за другим законом Кірхгофа:
.
Рівняння струмів для вузла 1:
Рівняння за другим законом Кірхгофа:
Підставами в рівняння (а) і (б) числові значення отримаємо:
,
.
Вирішивши цю систему, визначимо струми
:
;
.
1. Білецький А.Ф. Теорія лінійних електричних ланцюгів. - М. Радіо і зв'язок, 1986.
3. Качанов Н. С. та ін. Лінійні радіотехнічні пристрої. М. Воен. іздат. 1 974.