Метод складання і рішення рівнянь Кірхгофа
Покладемо, що в схемі, що містить "m" гілок до "n" вузлів, заданими є всі елементи і конфігурація, а шуканими - струми в гілках. Число невідомих при цьому дорівнює числу гілок.
Намети шлях розрахунку.
1). Вибираємо довільно позитивні напрямки струмів в гілках (зручно в гілках з джерелами напруг направити струми по стрілці ЕРС).
2). Складаємо рівняння 1-го закону Кірхгофа. Можливе складання "n" рівнянь виду.
Неважко помітити, що кожен ток увійде в два рівняння з протилежними знаками. Тому сума рівнянь тотожно дорівнює нулю, тобто одне з рівнянь випливає з n-1 інших. Отже, по 1-му закону Кірхгофа необхідно скласти n - 1 незалежних рівнянь.
3). Відсутні для визначення "m" невідомих струмів рівняння повинні бути записані по 2-го закону Кірхгофа. Їх необхідно мати m - (n - 1) = m - n + 1.
Якщо до всіх гілок застосувати закон Ома, то вийде "m" рівнянь виду:. де - напруга між вузлами i і р. Еk. Ik - ЕРС джерела і ток в к-ой гілки, спрямовані від вузла до вузла р. R - опір до другої гілки. Більш зручна запис:.
У систему рівнянь закону Ома входять "m" невідомих струмів Ik і n-1 невідомих потенціалів (потенціал одного вузла приймається рівним нулю). Якщо виключити ці невідомі потенціали, залишиться m - n + 1
рівнянь, що зв'язують ЕРС джерел з напругою на опорах, т. е. рівняння 2-го закону Кірхгофа. Для того, щоб рівняння були незалежними, необхідно, щоб в кожне наступне входила хоча б одна нова гілка. Практично зручно записувати рівняння для контурів, які не мають всередині гілок, т. Е. Для осередків.
4). Кількість необхідних рівнянь 1-го і 2-го законів Кірхгофа легко встановлюється по графу ланцюга. Для цього складається дерево графа. Раніше встановлено, що число гілок дерева графа якраз одно n - 1,
т. е. дорівнює числу необхідних і достатніх рівнянь 1-го закону Кірхгофа. Число необхідних і достатніх рівнянь 2-го закону Кірхгофа m - n + 1 дорівнює числу гілок зв'язку.
5). При розрахунку ланцюгів часто визначається потужність джерел і приймачів енергії. Слід враховувати, що повинен дотримуватися закон збереження енергії, внаслідок якого
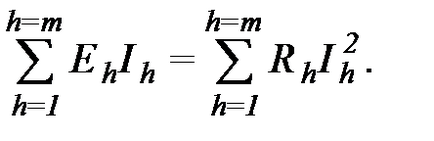
У лівій частині рівняння при збігу напрямків Еh і Ih твір позитивно, а при несовпаденіі- негативно.
6). При наявності в схемі джерел струму їх слід враховувати при запису рівнянь 1-го закону Кірхгофа. Віддається ними енергія враховується в лівій частині рівняння балансу потужностей.
7). Якщо струм визначено негативним, то його дійсне напрям протилежний прийнятому на початку розрахунку.
Метод контурних струмів (осередків).
Є одним з основних методів розрахунку складних ланцюгів. Він полягає в тому, що замість струмів в гілках визначаються на підставі 2-го закону Кірхгофа так звані контурні струми. При цьому ісключаютсяуравненія 1-го закону Кірхгофа.
Для незалежних контурів по 2-го закон Кірхгофа:
Виключимо струми внутрішніх гілок, висловивши їх через струми зовнішніх
Отримана система рівнянь містить три невідомих I1, I2, I3. через які можуть бути потім визначені I4 іI5.
Рівняння можуть бути записані відразу, якщо приписати кожному осередку деякий контурний струм, що співпадає зі струмом зовнішніх гілок. Тоді в кожному осередку алгебраїчна сума ЕРС дорівнює алгебраїчній сумі добутків
а) контурного струму даного осередку на суму опорів контуру;
б) контурних струмів кожної суміжній осередки - на опору суміжних галузей.
Правило знаків залишається таким же, як і при запису рівнянь 2-го закону Кірхгофа.
Загальний вигляд рівнянь для "n" контурів: де Rnn - сума опорів n-ой осередки, Rn2 - сума опорів гілки, загальною для n-ого і 2-го контурів,
Еn - алгебраїчна сума ЕРС n-ого контуру.
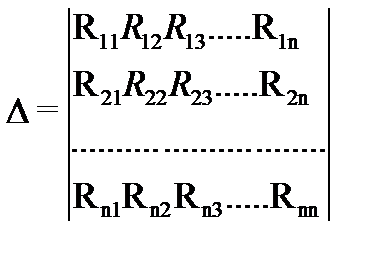
Отримана система може бути вирішена за допомогою визначників:
де
Якщо схема містить джерела струму, то можна прийняти ток кожного замикається по гілки будь-якого незамкнутого контура, що доповнює гілка з джерелом струму до замкнутого. Падіння напруги за рахунок такого струму на опорі контура враховується разом з падінням напруги від контурних струмів.
Метод вузлових потенціалів.
Цей метод дозволяє зменшити число рівнянь Кірхгофа за рахунок виключення рівнянь 2-го закону. На схемі приймаємо потенціал точки "О" рівним нулю.
Висловимо струми всіх гілок, що примикають до вузла "а" по закону Ома:
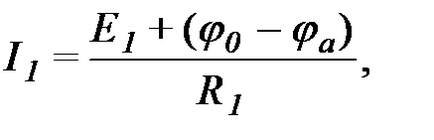
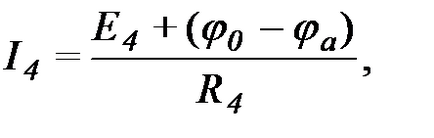
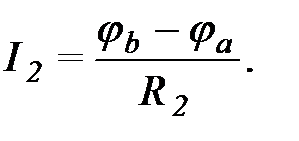
На підставі 1-го закону Кірхгофа: тобто .
Аналогічної виду рівняння можуть бути отримані для вузла 'b', а також для будь-якого вузла більш складної схеми.
Аналіз рівнянь показує, що для будь-якого вузла алгебраїчна сума добутків ЕРС на провідність всіх підключених до нього гілок дорівнює
а) потенціалу даного вузла, помноженому на суму провідностей підключених до нього гілок,
б) мінус твір потенціалів інших вузлів, помножених кожен на суму провідностей гілок, що з'єднують вузол з тим, для якого пишеться рівняння.
Якщо ЕРС спрямована до вузла, то Ek Gk входить в рівняння з "плюсом", від вузла - з "мінусом".
Джерела струму слід враховувати в лівій частині рівнянь з "плюсом", якщо вони спрямовані до даного вузла. Загальний вигляд рівнянь: де: G11 - сума провідностей гілок, підключених до 1-му вузлу, G12 - сума провідностей гілок, що з'єднують 1-й вузол з 2-м.
Рівняння записуються для (n - 1) вузлів і вирішуються, наприклад, за допомогою визначників. За отриманими вузловим потенціалом визначаються струми гілок за допомогою закону Ома.
Метод накладення (суперпозиції).
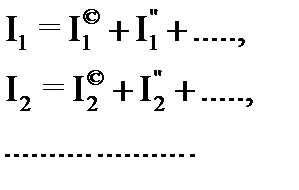
Рішення системи лінійних рівнянь однозначно визначає струми.
Припускаючи черзі в цьому ж ланцюзі наявність тільки однієї ерс при інших рівних нулю, можна для кожної ЕРС обчислити відповідні струми гілок, склавши рівняння:
Склавши рівняння почленно, отримаємо:
Отримана система має єдине рішення для невідомих і т.д.
З порівняння вихідних рівнянь і щойно отриманих слід, що рішення повинні збігатися, тобто
Таким чином, струм кожної гілки дорівнює алгебраїчній сумі часткових струмів, утворених дією кожної ЕРС окремо (принцип накладення).
На цьому заснований розрахунок ланцюгів методом накладення.
Напруга на ділянці кола з опором R.
тобто принцип накладення застосуємо і до напруженням.
Принцип накладення застосуємо також і до джерел струму. При цьому інші джерела струму відключаються.
Принцип накладення не застосовується для потужностей - квадратичних функцій струмів і напруг.
Перетворення електричних ланцюгів.
Різні перетворення застосовуються зазвичай спільно з іншими методами розрахунку. При цьому ланцюг залишається еквівалентної заданої, але розрахунок струмів значно спрощується.
Якщо ЕРС, діючи в одній гілці складного ланцюга / q / при відсутності інших ЕРС, викликає в іншій гілці / l / ток Il. то така ж ЕРС, діючи в галузі l при відсутності інших ЕРС, викличе в першій / q / такий же струм
Згідно з методом контурних струмів:
Так як для системи ток в галузі l визначається з де
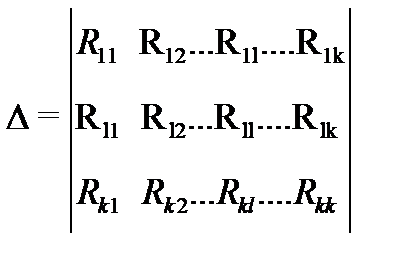
Загальні опору Rql і Rlq. рівні, тому що R12 = R21. R23 = R32 і т.д. Тому і відрізняється тільки тим, що рядки є стовпцями .Отже Принцип може бути застосований, наприклад, для визначення струмів в різних гілках схеми при одній ЕРС.