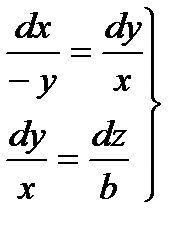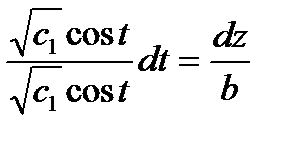Властивості градієнта - студопедія
1 0 Градієнт спрямований по нормалі до поверхні рівня (або до лінії рівня, якщо поле плоске).
2 0 Градієнт спрямований в бік зростання функції поля.
3 0 Модуль градієнта дорівнює найбільшою похідною по направленіювданной точці поля:
Ці властивості дають інваріантну характеристику градієнта. Вони говорять про те, що вектор gradU вказує напрямок і величину найбільшого зміни скалярного поля в даній точці.
Зауваження 2.1. Якщо функція U (x, y) є функція двох змінних, то вектор
лежить в площині oxy.
Нехай U = U (x, y, z) і V = V (x, y, z), що диференціюються в точці М0 (x, y, z) функції. Тоді має місце такі рівності:
а) grad () =; б) grad (UV) = VgradU + UgradV;
в) grad (U V) = gradU gradV; г) г) grad =. V;
д) gradU (= gradU, де. U = U () має похідну по.
Приклад 2.1. Дана функція U = x 2 + y 2 + z 2. Визначити градієнт функції в точці М (-2; 3; 4).
Рішення. Відповідно до формули (2.2) маємо
,
.
Поверхнями рівня даного скалярного поля є сімейство сфер x 2 + y 2 + z 2. вектор gradU = (- 4; 6; 8) є нормальний вектор площин.
Приклад 2.2. Знайти градієнт скалярного поля U = x-2y + 3z.
Рішення. Відповідно до формули (2.2) маємо
Поверхнями рівня даного скалярного поля є площині
x-2y + 3z = С; вектор gradU = (1; -2; 3) є нормальний вектор площин цього сімейства.
Приклад 2.3. Знайти найбільшу крутизну підйому поверхні U = x y в точці М (2; 2; 4).
Приклад 2.4. Знайти одиничний вектор нормалі до поверхні рівня скалярного поля U = x 2 + y 2 + z 2.
Рішення. Поверхні рівня даного скалярного Поля-сфера x 2 + y 2 + z 2 = С (С> 0).
Градієнт спрямований по нормалі до поверхні рівня, так що
. Визначає вектор нормалі до поверхні рівня в точці М (x, y, z). Для одиничного вектора нормалі отримуємо вираз
.
Приклад 2.5. Знайти градієнт поля U =. де і постійні вектори, r-радіус вектор точки.
тоді:
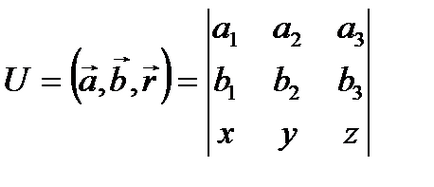
Приклад 2.6. Знайти градієнт відстані. де P (x, y, z) - вивчається точка поля, P0 (x0, y0, z0) - деяка фіксована точка.
Рішення. Маємо - одиничний вектор напрямку.
Приклад 2.7. Знайти кут між градієнтами функцій в точці М0 (1,1).
Рішення. Знаходимо градієнти даних функцій в точці М0 (1,1), маємо
; Кут між gradU і gradV в точці М0 визначається з рівності
Приклад 2.8. Знайти похідну по напрямку, радіус вектор дорівнює
Рішення. Знаходимо градієнт цієї функції:
Підставляючи (2.5) в (2.4), отримаємо
Приклад 2.9. Знайти в точці М0 (1; 1; 1) напрямок найбільшого зміни скалярного поля U = xy + yz + xz і величину цього найбільшого зміни в цій точці.
Рішення. Напрямок найбільшого зміни поля вказується вектором grad U (M). Знаходимо його:
І, значить,. Це вектор визначає напрямок найбільшого зростання даного поля в точці М0 (1; 1; 1). Величина найбільшого зміни поля в цій точці дорівнює
.
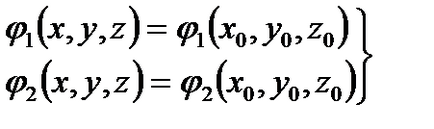
Приклад 3.1. Знайти векторні лінії векторного поля де-постійний вектор.
Рішення. Маємо так що
Диференціальні рівняння векторних ліній
Помножимо чисельник і знаменник першого дробу на х, другий-на у, третій- на z і складемо почленно. Використовуючи властивість пропорцій, отримаємо
. звідси xdx + ydy + zdz = 0, а значить
x 2 + y 2 + z 2 = A1. A1 -const> 0. Помноживши тепер чисельник і знаменник першого дробу (3.3) на з1. другий -на с2. третій на с3 і склавши почленно, отримаємо
. звідки з1 dx + c2 dy + c3 dz = 0
Шукані рівняння векторних ліній
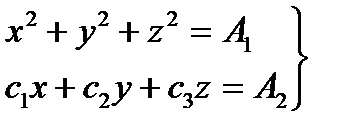
Ці рівняння показують, що векторні лінії виходять в результаті перетину сфер, що мають загальний центр на початку координат, з площинами, перпендикулярними вектору. Звідси випливає, що векторні лінії є колами, центри яких знаходяться на прямій, що проходить через початок координат в напрямку вектора с. Площини кіл перпендикулярні зазначеної прямий.
Приклад 3.2. Знайти векторну лінію поля проходить через точку (1,0,0).
Рішення. Диференціальні рівняння векторних ліній
звідси маємо