Визначення ефективної процентної ставки
Ефективна процентна ставка - це складна процентна ставка по кредиту, розрахована в припущенні, що всі платежі, необхідні для отримання даного кредиту, йдуть на його погашення.
Тобто, якщо в результаті отримання кредиту розміром S0 позичальник змушений здійснювати платежіR0, R1, R2. Rn в моменти временіt0 = 0, t1, t2. tn відповідно (сюди входять як платежі із самого кредиту, так і побічні комісії, страхові виплати і т.п.), то ефективна процентна ставкаi знаходиться зі співвідношення
Ефективна процентна ставка служить в першу чергу для порівняння між собою різних банківських пропозицій, і при її обчисленні точні дати здійснення платежів зазвичай невідомі. Тому, якщо платежі здійснюються через формально однакові проміжки часу тривалістю τ (щомісяця, щокварталу і т.д.), то формула (18.1) набуває такого вигляду:
Якщо всі платежі позичальника, за винятком, можливо, самого першого, однакові (R1 = R2 =. = Rn = R), то відповідно до формули (17.4) співвідношення для визначення ефективної процентної ставки буде таким:
На жаль, знайти точне значення ефективної процентної ставки навіть в такому порівняно простому випадку неможливо, тому доводиться його підбирати (найкраще - за допомогою спеціального чисельного методу). Як саме - про це піде мова в наступних параграфах.
Приклад Для кредиту з наступними умовами:
термін кредитування - 3 роки;
процентна ставка (будемо позначати її j) - 18% річних;
схема погашення кредиту - щомісячними рівними (ануїтетними) платежами;
комісія за організацію кредиту - 1% від його суми;
щомісячна комісія за ведення позичкового рахунку - 0,1% від суми кредиту
ефективна процентна ставка становитиме 22,8%. Для перевірки знайдемо значення всіх змінних, присутніх у формулі (18.3):
Підставляючи ці значення в (18.3), після скорочення на S0 легко переконуємося в справедливості рівності (якщо, звичайно, знехтувати похибкою заокруглень):
Перевірити вірність розрахунку ефективної процентної ставки можна за допомогою нашого кредитного калькулятора.
Приклад Кредит розміром 24 тисячі євро, виданий на два роки під 12% річних, погашається щомісячними платежами відповідно до диференційованої схемою. Комісія за організацію кредиту становить 1% від його суми. Крім того, кожен місяць з позичальника стягується комісія за ведення позичкового рахунку розміром 0,1% від суми кредиту. Нам потрібно знайти ефективну процентну ставку за даним кредитом.
Перш за все, побудуємо графік погашення кредиту (без урахування структури платежів). З § 11 ми знаємо, що платежі в рахунок погашення кредиту утворюють арифметичну прогресію з початковим членом
A1 = 124 + 0,12⋅112⋅24 000 = 1240 євро
-0,12⋅112⋅24 000⋅124 = -10 євро.
Крім того, при отриманні кредиту позичальник був змушений заплатити 0,01 · 24 000 = 240 євро, а кожен місяць з нього стягується комісія розміром 0,001 · 24 000 = 24 євро. Значить, графік платежів по кредиту має наступний вигляд:
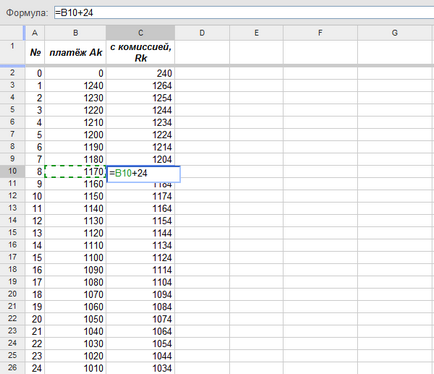
Значення стовпця «з комісією, Rk». за винятком самого першого (з індексом 0), збігаються з коефіцієнтами при степеняхx у функцііf (x), яку ми будемо використовувати в розрахунках. Для отримання першого коефіцієнта (при нульовій степеніx) потрібно з початкового платежаR0 = 240 відняти розмір кредиту (формула в лівому верхньому кутку):
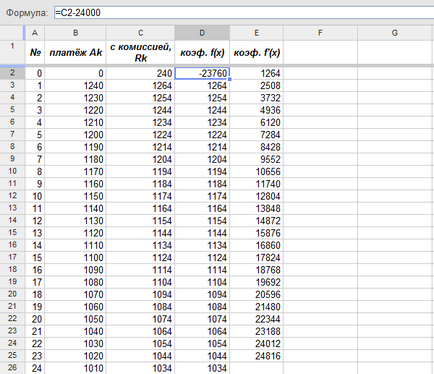
Нагадаю, якщо хто забув, що коефіцієнт з номером k у похідній рівний коефіцієнту з номеромk +1 у функцііf (x), помноженому наk +1.
Тепер, нарешті, можна застосувати метод Ньютона для знаходження місячного множника дисконтування (формула в лівому верхньому кутку):
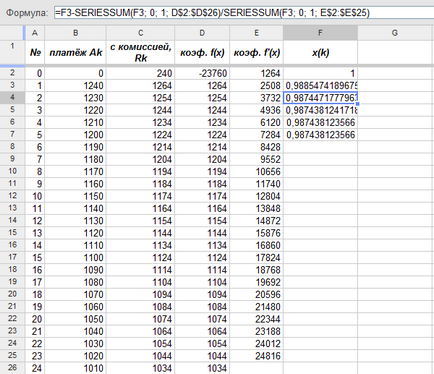
Одночасно з обчисленням місячного множника дисконтування визначаємо саму ефективну процентну ставку i:
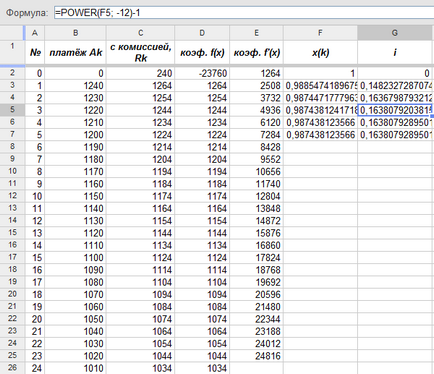
Як і в прикладі з попереднього параграфа, метод Ньютона привів нас до остаточної відповіді всього лише за п'ять обчислень: ефективна процентна ставка по даній кредиту приблизно дорівнює 16,38%, на 4,38% більше, ніж номінальна ставка.