Вектор швидкості точки
Векторний спосіб завдання руху точки.
Векторний, 2) координатний, 3) природний (або траєкторний).
Способи завдання руху точки
Для завдання руху точки можна застосовувати один з наступних трьох способів:
Нехай точка рухається по відношенню до деякої системи відліку (рис.1.1). Положення цієї точки в будь-який момент часу можна визначити,
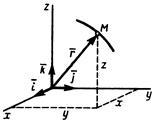
задавши її радіус-вектор. проведений з початку координат в точку. При русі точки вектор буде з плином часу змінюватися і по модулю, і за напрямком. Отже, є змінним вектором (вектором-функцією), що залежать від аргументу:
Це рівність і визначає закон руху точки у векторній формі, так як воно дозволяє в будь-який момент часу побудувати відповідний вектор і визначити місце розташування рухається точки.
Геометричне місце кінців вектора. тобто годограф цього вектора, визначає траєкторію рухається точки.
Аналітично, як відомо, вектор задається його проекціями на координатні осі. Для вектора буде:
де - координати точки. Тоді, якщо ввести одиничні вектори (орти) координатних осей, отримаємо для вектора вираз
Отже, залежність буде відома, якщо будуть задані координати точки як функції часу. Такий спосіб завдання руху точки (координатний) розглянемо нижче.
2.Коордінатний спосіб завдання руху точки.
Щоб знати закон руху точки, тобто її положення в просторі в будь-який момент часу, треба знати значення координат точки для кожного моменту часу, тобто знати залежності