Транспортна задача (5)
Лабораторна робота 2
Теоретична частина
Завдання про розміщення (транспортна задача) - це розподільна завдання, в якій роботи і ресурси вимірюються в одних і тих же одиницях. У таких завданнях ресурси можуть бути розділені між роботами, і окремі роботи можуть бути виконані за допомогою різних комбінацій ресурсів.
Прикладом типової транспортної задачі є розподіл (транспортування) продукції, що знаходиться на складах, по підприємствам-споживачам.
Стандартна транспортна задача - це задача розробки найбільш економічного плану перевезення продукції одного виду з декількох пунктів відправлення в пункти призначення. При цьому величина транспортних витрат прямо пропорційна обсягу перевезеної продукції і задається за допомогою тарифів на перевезення одиниці продукції.
Вихідні параметри моделі ТЗ:
n - кількість пунктів відправлення, m - кількість пунктів призначення.
- запас продукції в пункті відправлення () [од. тов.].
- попит на продукцію в пункті призначення () [од. тов.].
- тариф (вартість) перевезення одиниці продукції з пункту відправлення в пункт призначення [руб. / Од. тов.].
Шукані параметри моделі ТЗ
- кількість продукції, що перевозиться з пункту відправлення в пункт призначення [од. тов.].
- транспортні витрати на перевезення всієї продукції [руб.].
Етапи побудови моделі
Перевірка збалансованості завдання.
Сума запасів продукції в усіх пунктах відправлення повинна дорівнювати сумарній потреби у всіх пунктах споживання, тобто.
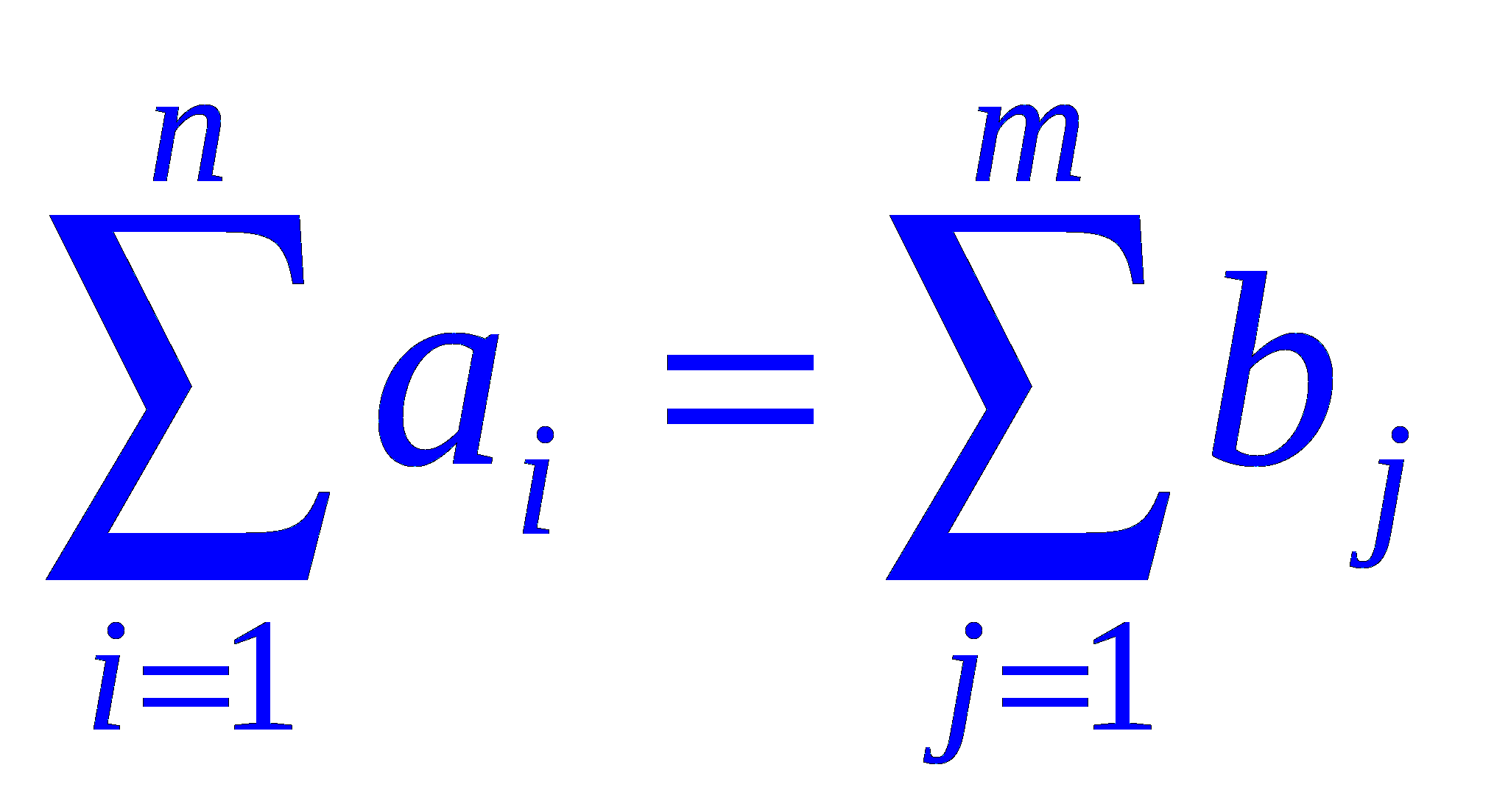
Транспортна задача називається збалансованою. якщо
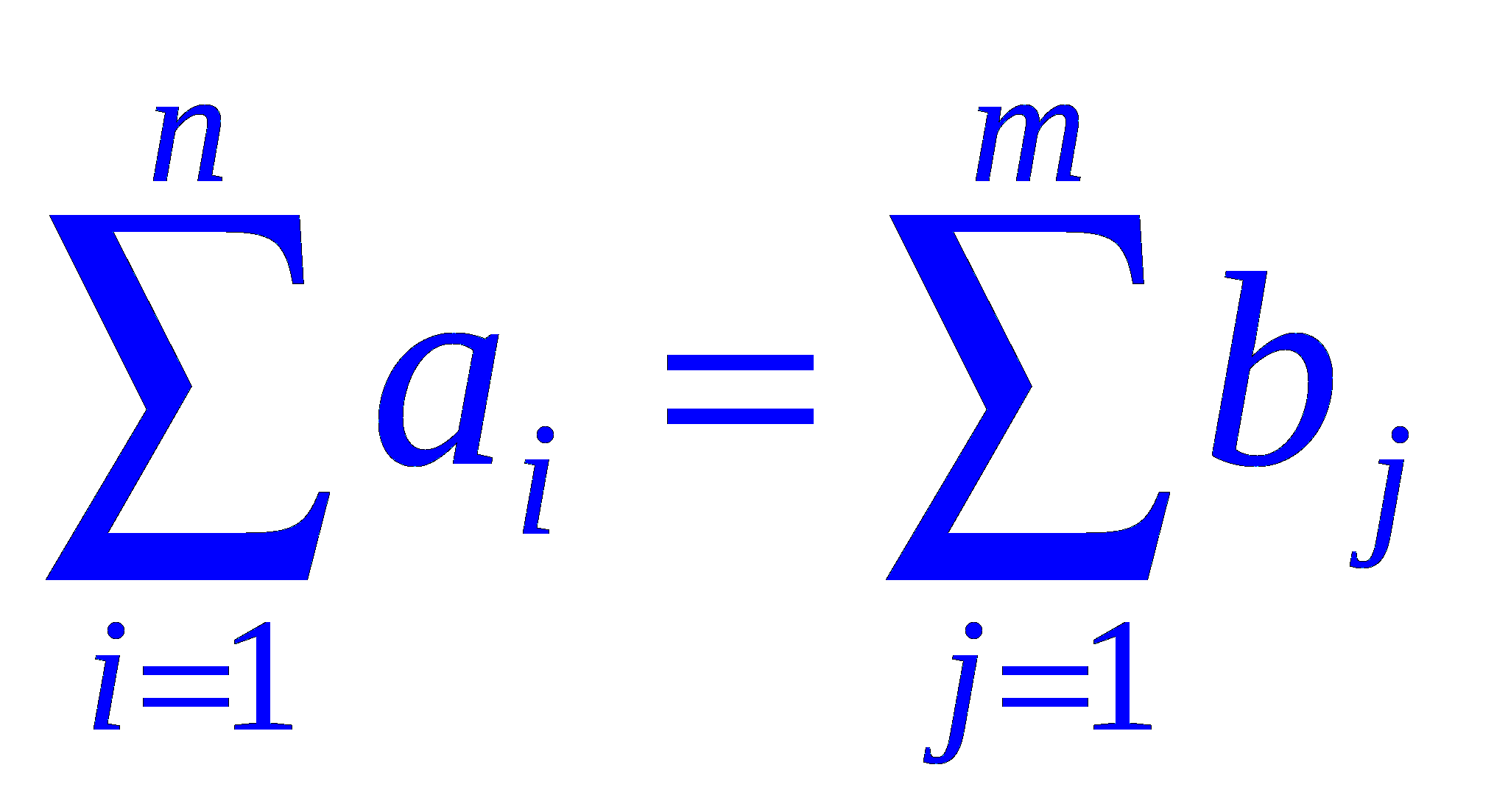
Оскільки обмеження моделі (0) можуть бути виконані тільки при збалансованій ТЗ, то при побудові транспортної моделі необхідно перевіряти умова балансу.
У разі, коли сумарні запаси перевищують сумарні потреби. необхідний додатковий фіктивний пункт споживання, який буде формально споживати існуючий надлишок запасів, тобто:
Якщо сумарні потреби перевищують сумарні запаси. то необхідний додатковий фіктивний пункт відправлення, формально який заповнює існуючий недолік продукції в пунктах відправлення:
побудова моделі
Побудуємо математичну модель для даної транспортної задачі.
1 крок. визначення змінних
Позначимо через [шт.] Кількість штучного товару, які будуть перевезені з i-го складу () в j-тий магазин ().
2 крок. Перевірка збалансованості завдання
Загальна кількість товару, необхідне для задоволення попиту одно: 45 + 90 + 50 = 185 і доступно: 25 + 50 + 35 + 75 = 185, отже, завдання збалансована.
3 шаг.Заданіе цільової функції
Формальна ЦФ, тобто сумарні витрати на всі можливі перевезення товару, що враховуються в моделі, задається виразом (0).
4 крок. завдання обмежень
Так як обсяги перевезення товару не можуть приймати негативні значення і повинні бути цілими числами, то з'являються умови невід'ємності і цілісності:
Нагадуємо, що символ називається квантором загальності (читається «для будь-якого»).
Таким чином, математична модель задачі представлена у вигляді: визначити обсяг, що забезпечує мінімальне значення функції:
при наявності обмежень:
Знаходження рішення транспортної задачі в Microsoft Excel
Знайдіть оптимальний план перевезень, використовуючи Microsoft Excel, для цього виконайте наступні дії:
Відкрийте програму Microsoft Excel.
Створіть екранну форму для введення умови задачі (Рис. 1).
Введіть вихідні дані (Таблиця 2) в екранну форму (Рис. 2).
Перевірте виконання умови балансу, для цього:
в осередок G10 введіть формулу СУММ (C10: F10), а в клітинку H9 введіть формулу СУММ (H3: H6);
якщо суми рівні, то в осередку H10 напишіть БАЛАНС (Рис. 3).
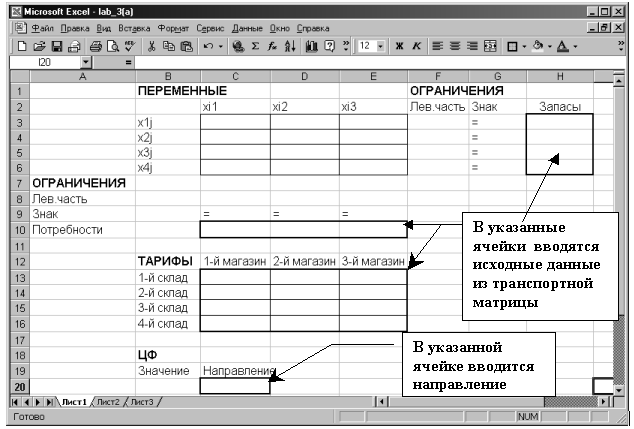
Мал. 1. Екранна форма транспортної задачі
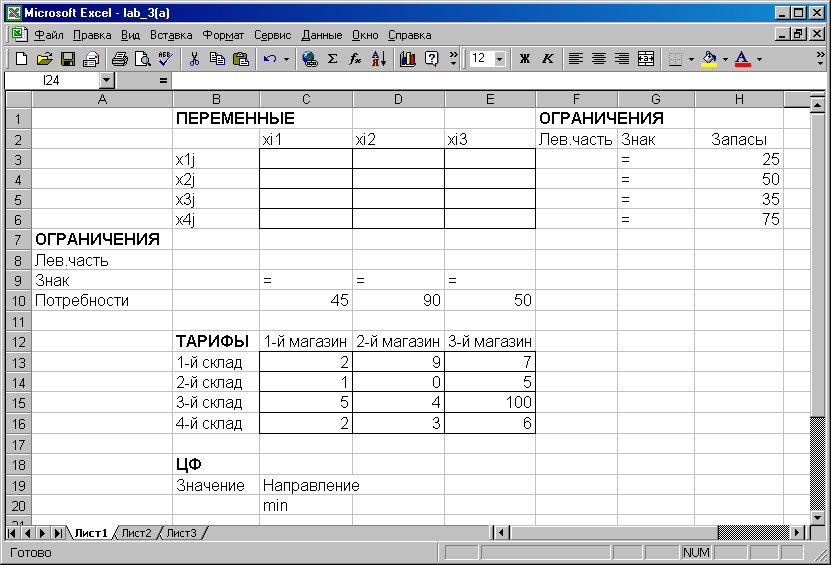
Мал. 2. Введення вихідних даних
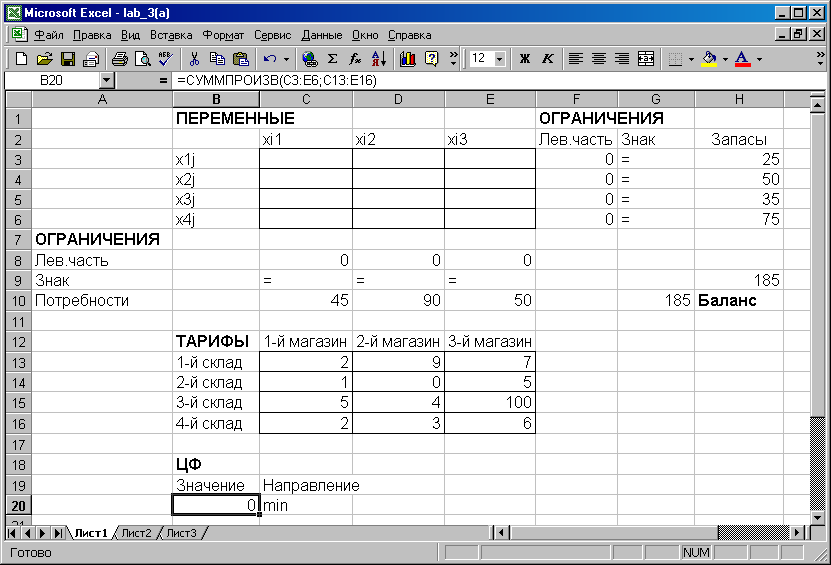
Мал. 3. Екранна форма після введення формул
Введіть залежності з математичної моделі (0) в екранну форму, скориставшись підказкою, наведеної нижче (Таблиця 3).
Формули екранної форми завдання
В екранній формі (Рис. 3) в осередках F3, F4, F5, F6, C8, D8, E8, B20 з'явиться поточне значення, обчислене по введеної формулою, тобто 0 (так як в момент введення формули значення змінних завдання нульові).
Здійсніть пошук рішення задачі, для цього:
зайдіть в меню СервісПоіск рішення;
в поле «Встановити цільову осередок» вкажіть цільову комірку $ B $ 20;
введіть напрямок оптимізації цільової функції, клацнувши один раз лівою клавішею миші по кнопці «мінімального значення»;
внесіть обмеження, що накладаються на умову задачі (Рис. 4);
запустіть «Пошук рішення». натиснувши на кнопку «Виконати».
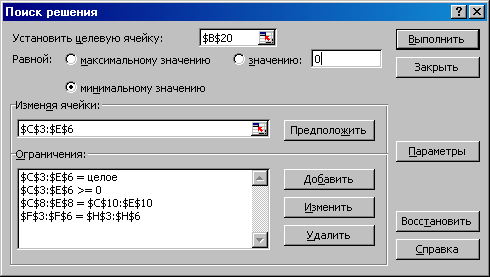
Мал. 4. Обмеження та граничні умови задачі
Проаналізуйте отриманий результат (Рис. 5).
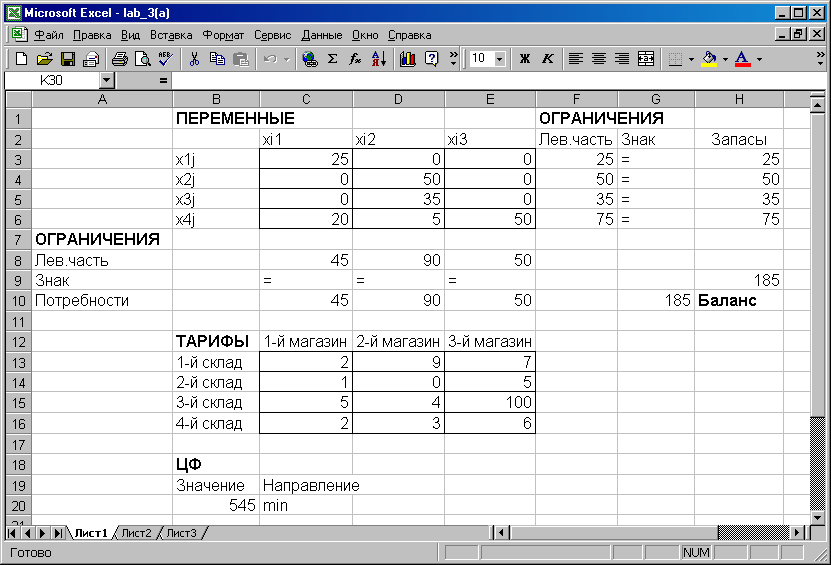
Мал. 5. Рішення транспортної задачі
Висновок. c 1-го складу в перший магазин треба перевезти 25 шт. товару, cо 2-го складу в другій магазин треба перевезти 50 шт. товару, c 3-го складу в другій магазин треба перевезти 35 шт. товару, c 4-го складу в перший магазин 20 шт. в другій магазин - 5 шт. в третій магазин - 50 шт. товару, загальна вартість перевезення буде дорівнює 545 рублів.
Збережіть файл у своїй папці з ім'ям lab_2.